1.2. Las características son las que cuentan
 |
Si hay algo que nos caracteriza a los matemáticos es que somos muy vagos. Por eso siempre estamos pensando cosas para tener que trabajar lo mínimo posible. Muchos teoremas, fórmulas y propiedades que utilizamos nos sirven para hacer los cálculos de una forma más simple y rápida.
Como verás en este apartado, hay muchas propiedades que nos permiten saber el valor de un determinante de una forma mucho más fácil que la que hemos visto hasta ahora, a veces, con un simple golpe de vista. Las propiedades que vamos a ver no solamente nos van a simplificar el cálculo, si no que nos van a permitir hallar determinantes de orden superior, para los que ya no hay una regla como en el caso de orden 2 y 3.
Vamos a enunciar la propiedad y poner un ejemplo numérico de lo que quiere decir cada una de ellas. Aunque el ejemplo sea de orden 2 ó 3, estas propiedades se cumplen para determinantes de cualquier orden. Cuando dé igual trabajar por filas que por columnas utilizaremos el término línea.
1) El determinante de una matriz es igual que el de su matriz traspuesta, es decir, 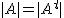 .
.
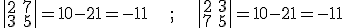
2) Si intercambiamos dos líneas de un determinante, el determinante cambia de signo, aunque vale lo mismo en valor absoluto.
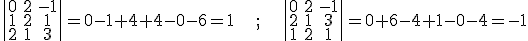
3) Un determinante con una línea formada por ceros es siempre nulo.
¿Recuerdas que dijimos que al desarrollar un determinante en todos los productos había un elemento de cada fila y de cada columna? Pues por eso un determinante donde una fila (o columna) sea entera de ceros hace que en todos los productos aparezca un cero y por tanto es nulo. Escribe un determinante de orden tres con esa característica y compruébalo.
4) Un determinante con dos líneas paralelas iguales vale cero.
Esta propiedad es consecuencia de la segunda y puedes ver un ejemplo en la última autoevaluación que hiciste en el apartado anterior.
5) Si multiplicamos una línea de un determinante por un número, el valor del determinante queda multiplicado por ese número.
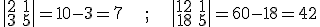
Como consecuencia de esta propiedad, si una línea es múltiplo de un número, podemos sacar factor común ese número y simplificar la línea. Y si multiplicamos un determinante por un número, sólo se multiplica una línea de ese determinante, a diferencia de lo que pasaba en las matrices. Comprueba tu mismo que se cumplen las igualdades 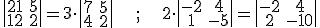 .
.
6) Si en un determinante, dos líneas paralelas son proporcionales, el determinante es nulo.
Esta propiedad es consecuencia de dos de las anteriores. Vamos a ver como, sin desarrollar, podemos ver que el determinante es nulo: 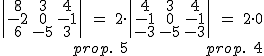
7) Si todos los elementos de una línea son suma de dos sumandos, el determinante puede descomponerse en la suma de otros de forma que en esa línea vayan los primeros sumandos en uno de los determinantes y los segundos en otro. Todas las restantes líneas son iguales a la del determinante original.
Esta es la propiedad más complicada de entender. Te ponemos un ejemplo.
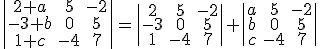
Observa que según esta propiedad, para poder sumar dos determinantes es necesario que todas las líneas sean iguales menos una, y la suma se realiza dejando igual las líneas comunes y sumando las dos desiguales.
8) Si una línea de un determinante es suma de líneas paralelas a ellas multiplicadas por números (lo que se llama una combinación lineal), el determinante es cero.
Esta propiedad se cumple gracias a las dos propiedades anteriores. Veámoslo en general para cualquier determinante de orden tres.
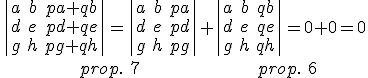
Compruébalo hallando el siguiente determinante en el que la tercera fila es la suma de la primera más el doble de la segunda. 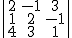
9) Si a una línea le sumamos una combinación lineal de las líneas paralelas a ella, el determinante no varía.
Partimos del determinante 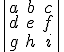 y si ahora le sumamos, por ejemplo, a la primera columna las otras dos multiplicadas por números, podemos ver que el determinante no varía.
y si ahora le sumamos, por ejemplo, a la primera columna las otras dos multiplicadas por números, podemos ver que el determinante no varía.
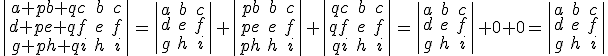
Comprueba ahora esta propiedad hallando los dos siguientes determinantes y viendo que da la mismo. En ellos le hemos sumado a la segunda fila la primera y la tercera.
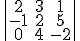 vale lo mismo que
vale lo mismo que 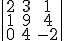
10) El determinante de un producto de dos matrices cuadradas, del mismo orden, es igual al producto de los determinantes de las dos matrices. Es decir 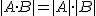 .
.
Consideremos las matrices 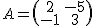 y
y 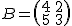 , entonces el producto sería
, entonces el producto sería
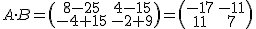
Y los determinantes cumplen |A·B| = -17·7-11·(-11) = -119+121 = 2.
|A|·|B| = (6-5)·(12-10) = 1·2 = 2 = |A·B|
Sin desarrollar, indica cuánto valen los siguientes determinantes.
1) 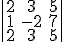 2)
2) 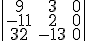 3)
3) 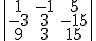 4)
4) 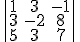
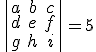 , utiliza las propiedades anteriores para calcular el valor de los siguientes determinantes.
, utiliza las propiedades anteriores para calcular el valor de los siguientes determinantes.
1) 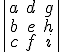 =
; 2)
=
; 2) 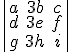 =
=
3) 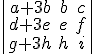 =
; 4)
=
; 4) 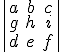 =
=
Si una línea de una matriz es igual o proporcional a otra, o si una línea es igual a la suma de otras paralelas multiplicadas por números, lo que equivale a decir que esa primera línea es linealmente dependiente de las restantes, a veces es fácil verlo a simple vista, pero otras no. El determinante nos lo fija directamente, ya que si es cero entonces es claro que hay algún tipo de dependencia entre las líneas de esa matriz. Sólo cuando no es igual a cero podemos estar seguros de que las líneas son independientes entre sí.