1.1. Empecemos por calcular el más fácil
 |
Antes de empezar con el concepto de determinante si debemos comentarte algo. El cálculo del determinante de una matriz es una herramienta que nos va a permitir resolver problemas más o menos cotidianos, pero es solamente eso, una herramienta.
Suponemos que recuerdas, por ejemplo, el método de sustitución para resolver un sistema de ecuaciones. Pasa algo parecido. Es decir, mientras que en muchas situaciones de la vida cotidiana te puedes encontrar cuadros de números, como viste en el tema anterior, nunca te vas a encontrar un determinante por la calle. Quizás por eso este tema te parezca un poco más abstracto, pero como verás en los temas que siguen, sin este concepto hay muchos problemas que sería muy complicado resolver.
El determinante de una matriz cuadrada es un número que se asocia a dicha matriz y que nos va a permitir, por ejemplo, saber si la matriz tiene o no inversa, o el número de soluciones de un sistema de ecuaciones.
Si tenemos la matriz 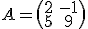 su determinante se representa de distintas formas:
su determinante se representa de distintas formas:
podemos escribir det(A), |A| ó 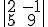 .
.
Como puedes ver por la última expresión, se escribe igual que una matriz pero se limita por líneas rectas en lugar de por paréntesis.
El determinante de una matriz cuadrada de orden dos es igual al producto de los elementos de la diagonal principal menos los de la diagonal secundaria. Es decir:
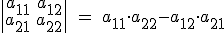
Así el determinante que hemos visto antes sería 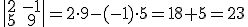
Si te fijas en los subíndices que aparecen en la definición del
determinante anterior puedes observar que en cada producto hay un
elemento de cada fila (observa el subíndice primero de cada término en
ambos productos) y un término de cada columna (fíjate ahora en los
segundos subíndices de cada término a). Esta característica se va a
cumplir en todos los determinantes.
- El valor del determinante
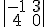 es
.
es
. - Para que el valor del determinante
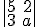 sea 4 es necesario que a valga
.
sea 4 es necesario que a valga
.
En la siguiente ventana tienes un archivo de Flash en el que puedes ver dos métodos de recordar cómo se desarrolla. El más utilizado es el segundo, aunque en el primero viene una regla que quizás te sea más clara, pero recuerda que lo que ves en el primer método es una ayuda para recordar el desarrollo, es decir, no tiene ningún sentido un determinante con cinco columnas y tres filas.
Montaje tomado del Banco de Imágenes y Sonidos del Instituto de Tecnologías Ecucativas (antiguo ISFTIC).
En la siguiente escena de Descartes puedes ver ejemplos resueltos de determinantes de orden 2 y 3. Intenta tú primero aplicar los cálculos y después puedes comprobar con la escena si tienes bien los cálculos.
Archivo creado por Alfredo Pena Iglesias, con Descartes, bajo licencia Creative Commons (CC) BY-NC-SA
1) El valor del determinante 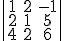 vale
.
vale
.
2) Al desarrollar el determinante 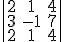 obtenemos
como resultado.
obtenemos
como resultado.
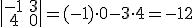 .
.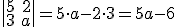 si queremos que sea 4, tendremos 5a-6=4 de donde, 5a=4+6 = 10 y por tanto a = 10/5 = 2.
si queremos que sea 4, tendremos 5a-6=4 de donde, 5a=4+6 = 10 y por tanto a = 10/5 = 2.