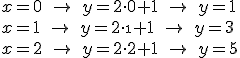2. Las funciones cuya gráfica es una recta
Ejemplo o ejercicio resuelto
 |
| 3. Imagen de timparkinson bajo licencia Creative Commons |
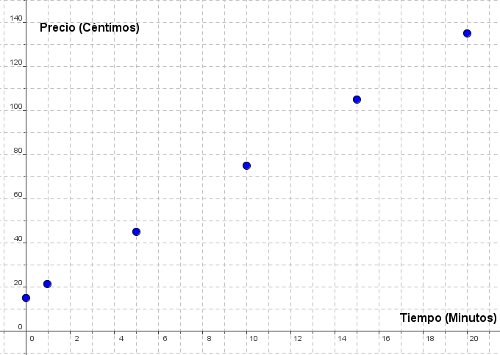
Otra situación habitual: el teléfono móvil. ¿Cuánto se paga? ¿Puedo encontrar una función que me dé el dinero que tengo que pagar según el tiempo que hable?
Patricia tiene contratada una tarifa para su móvil particular con la compañía Yellow Card. Le cobran 15 céntimos por el establecimiento de llamada y 6 céntimos por minutos, aunque facturan por segundos, es decir, si hablas medio minuto pagas 3 céntimos.
¿Cuál es la función que da el precio a pagar por Patricia según el tiempo hablado? ¿Podemos ver una gráfica de esta situación?
Actividad
Ejemplo o ejercicio resuelto
 |
| 4. Imagen de soylentgreen23 bajo licencia Creative Commons. |
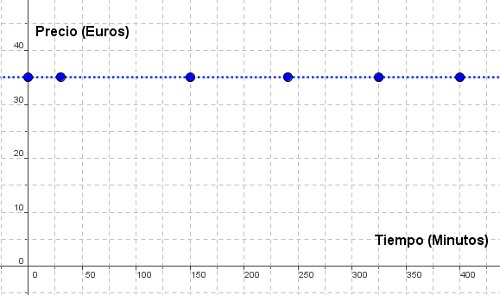
Pero otra oferta de la compañía Yellow Card es la tarifa plana de voz por 35 €/mes, incluyendo todas las llamadas a fijos y móviles de cualquier compañía, que justamente es la tarifa que tiene Patricia en el móvil del despacho de la notaría.
¿Cómo sería ahora la función?
Actividad
Las funciones que gráficamente se representan mediante una recta son:
- La función afín: y = mx + n, con m y n números reales.
- La función lineal o de proporcionalidad: y = mx, con m un número real, que pasa por el origen de coordenadas.
- La función constante: y = n, con n un número real, que es una recta horizontal.
Por ejemplo:
- y=2x sería una función de proporcionalidad.
- y = 3x - 4 sería una función afín.
- y = 8, sería constante.
Como puedes ver, las funciones lineales y constante, son casos particulares de la función afín.
En la función lineal, n = 0 y en la constante, m = 0.
AV - Reflexión
Realiza la siguiente actividad en la que debes asociar cada gráfica con el tipo de función que es:
Ejemplo o ejercicio resuelto
Para representar este tipo de funciones, sólo tenemos que darle dos o tres valores a "x" y calcular el valor que le corresponde en la "y". Como deben quedar alineados, bastará con unirlos después mediante una recta.
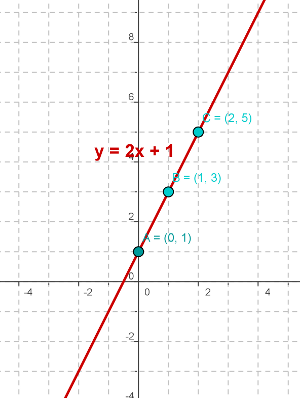
Por ejemplo, vamos a representar la función y = 2x +1.
Si aún no lo tienes claro, puedes ver el ejemplo del siguiente vídeo:
AV - Reflexión
En la siguiente escena debes practicar con la representación de estas funciones. Aparecen dos puntos y debes moverlos y colocarlos en el lugar adecuado para que la recta coincida con su gráfica.
Applet Descartes de Joaquín García Mollá bajo licencia Creative Commons.