2.1. Lo que distingue una de otra.

 

 
 5. Imagen de Villamota bajo licencia Creative Commons

Ya hemos visto que las funciones que se representan mediante una recta tienen como expresión general

y = mx + n.

 

Por tanto, lo que distingue una función de otra son los números "m" y "n", y puesto que distinguen y hacen que sean diferentes, habrá que bautizarlos de alguna manera. Pues sí, tienen nombre. El coeficiente "m" que multiplica a la x se llama pendiente de la recta y el "n" ordenada en el origen.

En las siguientes escenas vamos a ver el significado de estos dos parámetros.

 


 

Comenzamos con la pendiente de la recta

 

Mueve el control "a" y observa lo que pasa en la recta cuando variamos su pendiente.

Please install Java 1.4 (or later) to use this page.
AV - Pregunta Verdadero-Falso
Contesta a las siguientes cuestiones manipulando antes la escena.


1) Si la pendiente es un número positivo, la recta siempre crece.

Verdadero Falso


2) Si la pendiente de la recta es un número negativo, la recta es decreciente

Verdadero Falso


3) Mientras mayor sea el valor absoluto de la pendiente, la recta va creciendo más lentamente.

Verdadero Falso


4) la función y =4x crece más rápidamente que la función y = x +4

Verdadero Falso
Icono de iDevice AV - Reflexión

En la siguiente escena debes unir cada gráfica con el tipo de pendiente que tiene.

 

This browser does not have a Java Plug-in.
Get the latest Java Plug-in here.
Icono IDevice Objetivos

El valor de la pendiente de una recta coincide con el valor de la tangente del ángulo que forma dicha recta con el eje horizontal o eje de abscisa.

La tangente es una de las tres razones trigonométricas de un ángulo, y conociendo su valor, podemos determinar el ángulo con ayuda de una calculadora, a través de la función inversa de la tangente o arcotangente.

Por ejemplo, si la tangente de un ángulo es 2, pulsamos el botón de función inversa, después el de tangente e introducimos la cifra, 2, y obtenemos que el ángulo en cuestión es 63.4º


Ordenada en el origen

 

Flores con tallos atravesados por gruesas espinas.
6. Imagen de cristal cosmico bajo licencia Creative Commons

 

 

En la siguiente escena, tienes una función en la que podemos modificar el coeficiente "n", o sea, la ordenada en el origen.

Si mueves el control, podrás ver que la recta siempre corta al eje de ordenada (eje Y) en el punto que coincide con el valor de n.

 

 

 

 

 

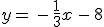Please install Java 1.4 (or later) to use this page.
Icono de IDevice de pregunta AV - Pregunta de Elección Múltiple
1) La recta corta al eje y en el punto:
  
y=8
y = - 8

2) La recta y = 2x, corta al eje Y en:
  
Y = 0
No corta al eje Y
Y = 2

AV - Pregunta de Selección Múltiple

Señala  todas las posibles respuestas que son ciertas con la función que te indicamos.

 

1) La función y = -3x + 1

Es decreciente
Tiene como pendiente 1
Corta al eje Y en 1
Es creciente



2) La función y = 4x - 2
Tiene como pendiente 4 y ordenada en el origen 2
Tiene como pendiente 4 y corta al eje y en - 2
Es creciente y tiene ordenada en el origen -2
Es creciente y corta al eje y en 4



« Anterior | Siguiente »