1. La proporcionalidad se hace función.
¿Recuerdas cuando en el tema 1 de la primera unidad le pegamos un repasito a la proporcionalidad?
 |
| 1. imagen de ferran pestaña bajo licencia Creative Commons |
Había magnitudes directamente proporcionales e inversamente proporcionales. La diferencia entre ellas era que en las directas, si una magnitud se multiplicaba por un número, la otra quedaba también multiplicada por dicho número, mientras que en las inversas, la segunda magnitud quedaba dividida por ese número.
Por ejemplo, la altura y la sombra eran magnitudes directamente proporcionales, pues si un pájaro de 50 cm da una sombra de 20 cm, un árbol de 2 metros ( 200 cm) dará una sombra de 80 cm; cuatro veces la del pájaro.
Otro ejemplo claro de magnitudes directamente proporcionales lo tenemos en el precio que pagamos y la cantidad que compramos. Así, si el kilo de salchichón está a 3 €, si compro un kilo pagaré 3 €, si compro dos, 6, y así podríamos seguir.
Pues, vamos a seguir; vamos a hacer una tabla con varias cantidades y los precios que habría que pagar.
| Kilos de salchichón |
1 |
2 | 5 | 6.5 | 8 |
0.5 |
3 |
| Precio a pagar |
3 | 6 | 15 | 19,5 | 24 | 1,5 | 9 |
Y ahora vamos a representar esos valores. Vamos a llamar "X", a la cantidad, en kilos, que compro de salchichón, e "Y", al precio que pago:
Mueve los puntos en la escena para que estén en el lugar que les corresponde.
 |
| 2. Imagen de imerelo bajo licencia Creative Commons |
Si lo has colocado bien, deben haberte quedado alineados, o sea, formando una línea recta, ¿no?
Por otro lado, si a "x" le habíamos llamado "kilos de salchichón" y a "y", "precio en €", se ve a simple vista que la relación entre las dos incógnitas es:
y = 3·x
Pues bien, si dos magnitudes son directamente proporcionales, la función que relaciona a ambas tendrá esa forma y su representación gráfica será una recta que pasa por el origen de coordenadas.
Si dos magnitudes, x e y son directamente proporcionales, la función que las relaciona será de la forma y = m·x. La gráfica es una recta que pasa por el punto (0,0)
A m se le llama pendiente de la recta, y es también la constante de proporcionalidad.
Verdadero Falso
Verdadero Falso
3)
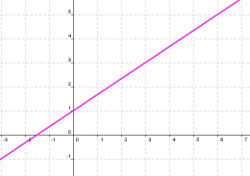
La gráfica corresponde a una función de proporcionalidad
Verdadero Falso
4)
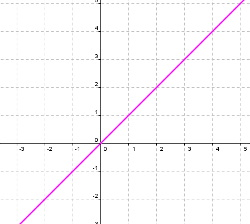
La gráfica corresponde a una función de proporcionalidad.
Verdadero Falso