2.2 Variaciones sobre la misma tabla
 |
| 8. Imagen de qutter bajo licencia Creative Commons |
Ya que conocemos la tabla, imagino que algunas cuestiones se te habrán pasado por la cabeza:
- ¿Y si quiero calcular la probabilidad de que la variable sea mayor que un valor concreto?
- ¿Puede haber números negativos?
- ¿Y si queremos calcular la probabilidad de que esté entre dos valores?
- ¿Y si la media y la desviación típica no son 0 y 1 respectivamente?
Pues a todo esto vamos a responder en este apartado del tema, y vamos a empezar por la última pregunta, viendo cómo cualquier distribución normal se puede transformar en una Normal de media 0 y desviación típica 1.
¿Te acuerdas de Jorge? Está equipando la cocina del piso que se ha comprado y entre otras cosas está ahora comparando lavavajillas. Entre los diverso folletos, está ojeando el de la marca electro-elec, y ahí ve la siguiente información sobre la vida útil del lavavajillas: "vida media: 14,6 años. Desv. típ: 0,5"
Jorge se dice, -si suponemos que la vida útil del lavavajillas se distribuye según un modelo normal, ¿qué probabilidad tengo de que como mucho me dure 16 años?
Si definimos X = tiempo de vida del lavavajillas, tenemos que X ~ N( 14,6 ; 0,5). Pues bien, si restamos el valor de la media, tenemos una nueva variable con media 0 y si dividimos entre la desviación típica, obtenemos otra nueva variable con desviación típica 1.
Así, la variable 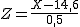 sigue una distribución N(0,1).
sigue una distribución N(0,1).
Por tanto, para dar respuesta a la cuestión que se nos plantea, hacemos esa transformación en la variable y en el valor del que queremos determinar la probabilidad.
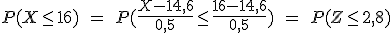
Para finalizar nos queda buscar 2,8 en la tabla y obtenemos que dicha probabilidad es: 0,9974
Para transformar una variable aleatoria normal en Normal N(0,1), primero se le resta la media de la variable, y el resultado se divide entre la desviación típica:
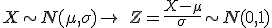
A este proceso se le llama tipificar la variable.
 |
| 9. Imagen de Chesi - Fotos CC bajo licencia Creative Commons |
Siguiendo con el lavavajillas que Jorge se va a comprar, ha visto que la probabilidad de que le dure menos de 16 años es muy grande, pero ¿y de que le dure más de 15?
Ahora la cuestión es que tiene que calcular la P( X > 15), o haciendo ya el proceso de tipificar ( recuerda restar 14,6 y dividir entre 0,5), P(Z > 0,8) ¿Y cómo se hace esto, si en la tabla siempre viene para menor?
Pues muy fácil, el suceso contrario a Z > 0,8 es Z ≤ 0,8, y este suceso sí que se puede calcular a través de la tabla. Además, si recuerdas del primer tema del bloque, la probabilidad del suceso contrario es 1- probabilidad del suceso:
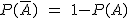
Por tanto, P(Z > 0,8) = 1 - P( Z ≤ 0,8) = 1 - 0,7881 = 0,2119. Luego no debe confiar demasiado en que le dure más de 15 años.
Siguiente cuestión. Ahora Jorge en vista del resultado que ha tenido, se pregunta un poco desolado, ¿será pequeña la probabilidad de que dure menos de 13 años?
Ahora habría que calcular la probabilidad P(X < 13), y haciendo el proceso de tipificar, ésta se transforma en P( Z < -3,2). Un número negativo. ¿Y si en la tabla sólo hay positivos?
Fíjate en el siguiente applet:
Applet Descartes modificado del original de Francisco Artigues Estarella publicado en la web Descartes bajo licencia Creative Commons
En el control valor_de_-z, puedes poner el valor que desees. La probabilidad que queremos calcular es el área de la región coloreada en turquesa que parece en la parte izquierda A. Si te fijas, en cada momento ese valor coincide con la región coloreada de amarillo y a su vez, si te fijas en la pantalla de la derecha, B, esa región es la opuesta de la región coloreada en verde.
Luego: Área Turquesa = Área Amarilla = 1 - Área Verde
Y ese Área Verde, ya lo podemos calcular en la tabla pues es el área de Z menor que el mismo valor positivo.
Por tanto, P( Z < -a ) = 1 - P(Z < a ).
Así que ya tenemos la respuesta a nuestra cuestión. P( X < 13) = P(Z< -3,2) = 1- P(Z < 3,2) = 1 - 0,99931 = 0,00069. Por tanto, la probabilidad de que el lavavajillas nos dure menos de 13 años es prácticamente nula, 0,069%.
Si queremos calcular la probabilidad de Z mayor que un número negativo, viendo nuevamente que es el suceso contrario al menor tendríamos que:
P(Z > -a) = 1 - P( Z < -a) = 1 - [ 1 - P(Z< a) ] = P (Z < a).
La última cuestión. Calcular una probabilidad entre dos valores. ¿Cuál sería la probabilidad de que el lavavajillas durara más de 14 años pero menos de 16?
Nuevamente te proponemos que observes la siguiente escena e intentes ver lo que ocurre:
Applet Descartes modificado del original de Francisco Artigues Estarella publicado en la web Descartes bajo licencia Creative Commons.
En los controles z1 y z2 puedes introducir los valores que desees para los extremos del intervalo. Pongas los valores que pongas, puedes ver en la pantalla de la derecha que la zona coloreada en turquesa es el área que queremos calcular.
Nuevamente tenemos que intentar relacionar esa área con la que nos ofrece la tabla de probabilidades, la de Z menor que un valor. Fíjate que en la escena de la izquierda tenemos coloreada las regiones Z < z2 en amarillo y Z < z1 en rojo y si te fijas bien lo que le falta al rojo para ser igual que el amarillo es precisamente la región turquesa, la que va de z1 a z2. Esto es lo mismo que decir que el área de la región turquesa es igual al área amarilla menos el área roja.
Luego: Área Turquesa = Área Amarilla - Área Roja, y esas dos las calculamos en la tabla o haciendo la transformación anterior si el valor es negativo.
Por tanto, P(a < Z < b ) = P( Z < b ) - P( Z < a)
En el lavavajillas de Jorge, tendríamos que P( 14 < X < 16) = P( X < 16 ) - P ( x < 14). Tipificando cada valor, esta probabilidad es igual a:
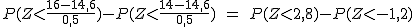
El primer valor se obtiene de la tabla y el segundo como es negativo, hacemos 1 - P( Z < 1,2).
Así, el resultado es: 0,9974 - ( 1 - 0,8849) = 0,9974 - 0,1151 = 0,8464. Luego hay una probabilidad bastante alta de que el lavavajillas dure entre 14 y 16 años.
 |
| 10. Imagen de bandita bajo licencia Creative Commons. |
Cálculo de probabilidades en una distribución Normal.
Si "a" es un número positivo y Z sigue una distribución N(0,1):
- P(Z < a) → A partir de la tabla de probabilidades de una distribución N(0,1)
- P(Z > a) = 1 - P( Z < a)
- P(Z < -a) = 1 - P( Z < a)
- P(Z > -a) = P ( Z < a )
- P(a < Z < b) = P(Z < b) - P(Z < a)
Ahora te toca a ti. Calcula las siguientes probabilidades usando las propiedades vistas arriba y la tabla de probabilidades de la distribución Normal N(0,1):
1. Z sigue una distribución N(0,1). Calcula:
- P(Z ≥ 0,32)
- P(Z ≤ 0)
- P ( Z > 0,7 )
- P ( -0,51 ≤ Z ≤ 0,51)
- P (Z > - 2,63)
2. Si X es N( 5,2 ), ¿cuál es la probabilidad de que X sea mayor o igual que 13,5?
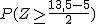 = P ( Z ≥ 4,25 ) = 1 - P ( Z < 4,25 ) = 1 - 1 = 0.
= P ( Z ≥ 4,25 ) = 1 - P ( Z < 4,25 ) = 1 - 1 = 0.