2.1 Lo corriente se distribuye así
 |
| 5. Imagen de Arenamontanus bajo licencia Creative Commons |
Y ahora ya sí, ha llegado el momento de conocer con todo lujo de detalles a esta distribución continua:
Una variable aleatoria continua X sigue una distribución normal de media μ y desviación típica σ, y se representa X ~ N(μ,σ) si se cumple que su función de densidad viene dada por:
La gráfica de esta función es similar a esta:
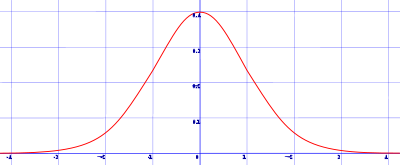
¿Entiendes ahora por qué se le llama la campana de Gauss?
Para saber más
¿Te has recuperado ya del susto? Bueno, no te preocupes que tampoco es que tengamos que utilizar ese pedazo de función para lo que nos interesa.
Ya hemos comentado que en estas distribuciones, la probabilidad de un intervalo se calcula cómo el área que hay bajo la curva dentro de ese intervalo.
Matemáticamente, esto se hace usando el concepto de integral, algo similar a la operación contraria de la derivada, pero para esta función es tan sumamente complicado que se utilizan otras herramientas para calcular estas probabilidades, aunque en el fondo de esos cálculos están las integrales.
En la siguiente escena, aparece representada la función de densidad de una distribución normal. En los controles "media" y "desv. tip" puedes introducir el valor que quieras de los dos parámetros de la distribución normal y colocando el control comenzar en 1, puedes ver sombreada una parte de esa distribución y dos puntos P y Q que puedes mover libremente. Además, en la esquina superior izquierda, aparece el valor del área de la región sombreada.
Applet Descartes de Ricardo Gutiérrez Ibáñez bajo licencia Creative Commons
AV - Reflexión
Contesta a las siguientes cuestiones manipulando la escena anterior:
- ¿Qué efecto produce sobre la función de densidad aumentar la media? ¿Y disminuirla?
- ¿Qué efecto produce sobre la función de densidad aumentar la desviación típica de la Normal? ¿Y disminuirla?
- Si X es N(0,1), ¿Cuál es la probabilidad de que X esté entre 2,1 y 3,5?
- Si X ~ N(0,1), calcula P(-3<X<0)
- Si X ~ N(0,1), calcula P(X ≥ -1) (Usa el zoom y aleja el punto Q)
- Si X ~ N(1,5 ; 0,6), calcula P(-2<X<2)
- Si X ~ N(-0,5 ; 1,5), calcula P(-2<X<2)
- Si X ~ N(8 , 2), calcula P(0≤X≤10) (Usa el zoom para ver la función)
- Si X ~ N(8 , 2), calcula P(X≥0)
- Si X ~ N(3 ; 0,5), calcula P(X<3)
- Si X ~ N(-2; 0,6), calcula P(X<-2)
Curiosidad
 |
| 6. Imagen de conanil bajo licencia Creative Commons |
Si te fijas bien en la gráfica de esta función, puedes ver que:
El dominio es el conjunto de todos los números reales.
Respecto a la media, la función es simétrica.
Tiene asíntota horizontal y = 0, tanto cuando x se va a -∞ como a +∞.
La función es creciente hasta que x llega al valor de la media y decreciente a partir de él. Por tanto, en x = μ la función alcanza su máximo.
Otra propiedad curiosa que cumple esta distribución es que las tres medidas de centralización coinciden, es decir, moda, mediana y media coinciden en el valor de μ.
Y ahora dirás, -vale muy bien, pero en la escena anterior la media solo llega hasta 10, ¿y si tengo que resolver una cuestión en la que la media sea mayor? o, y si no tengo esa escena, ¿cómo calculo una probabilidad de una distribución normal?
Pues tienes toda la razón, nos faltan recursos.
Existen tablas donde están calculadas las áreas para distintos valores de x en una distribución normal, pero ojo, en una distribución N(0,1), pero como vamos a ver en el siguiente apartado, cualquier distribución normal se puede transformar en una del tipo N(0,1).
Ejemplo o ejercicio resuelto
 |
| 7. Imagen de skpy bajo licencia Creative Commons. |
Vamos a familiarizarnos antes de seguir con esta tabla y cómo hay que usarla. En el enlace, te puedes descargar la tabla de valores de la distribución Normal N(0,1).
Lo primero que tienes que observar es que con esta tabla se calculan probabilidades del tipo P(Z≤a), donde Z representa la variable aleatoria que sigue la N(0,1) y "a" el valor extremo. Es decir, se calcula el área de la zona dibujada en azul.
Por ejemplo, vamos a calcular la probabilidad de que si Z es una variable N(0,1), un valor tomado al azar sea menor que 1,37.
Para calcularla, en la columna donde pone z0 hemos de buscar la fila en la que aparece el valor entero y la primera cifra decimal, es decir, 1,3. Una vez encontrado, nos vamos a las columnas y buscamos en el encabezamiento la segunda cifra decimal, o sea, donde aparezca 0,07.
El lugar donde se cruzan esas dos búsquedas me indica la probabilidad. En nuestro caso, aparece, 0,9147.
Luego P(Z ≤ 1,37) = 0,9147.
Si te ha quedado alguna duda, viendo la siguiente presentación seguro que se te aclaran.
Ve pulsando sobre la presentación para avanzar:
AV - Actividad de Espacios en Blanco
Calcula las siguientes probabilidades a partir de la tabla.
Usa la coma (,) para escribir los decimales.
P(Z ≤ 0,95) =
P(Z ≤ 3,14) =
P(Z ≤ 1) =
P(Z < 2,92) =
P(Z ≤ 3,07) =