1. Cuando el cambio es continuo
¿Recuerdas que al empezar los temas de estadística dividíamos las variables estadísticas en dos tipos, discretas y continuas?
Así por encima, las variables discretas eran las que tomaban valores aislados mientras que las continuas eran las que podían tomar cualquier valor entre dos concretos.
Pues bien, en el cálculo de probabilidades ocurre lo mismo. Ya en el tema anterior has visto que muchos experimentos aleatorios se pueden transformar en variables aleatorias, siempre que el resultado del experimento se pueda expresar mediante un número, pero en todos los casos que vimos, las variables que nos salían eran discretas. Sólo podían tomar algunos valores. Pero, esto no siempre es así, ¿no?
Imagínate que al azar elijo la primera persona que se me cruza por la calle, y me pregunto: ¿cuánto medirá?
Las respuestas podrían ser muchas. Infinitas incluso. Bueno, pues ejemplos como éste, nos van a llevar al concepto de variable aleatoria continua.
 |
| 1. Imagen de foxspain bajo licencia Creative Commons |
Una variable aleatoria es continua si al realizar el experimento aleatorio, entre cada dos valores, el número de valores que puede tomar es infinito.
Por ejemplo, la altura de una persona, la longitud del dedo índice, el peso de un perro o el caudal de un río.
 |
| 2. Imagen de j.o.h.n. walker bajo licencia Creative Commons |
Imagínate que hemos recogido los datos de la altura de 50 personas y los hemos anotado en esta tabla:
| 1,65 | 1,84 | 1,57 | 1,77 | 1,70 |
1,54 | 1,94 |
1,65 |
| 1,63 | 1,79 | 2,00 | 1,83 |
1,53 |
1,85 |
1,53 |
2,06 |
| 1,97 | 1,67 | 2,01 | 2,02 | 1,62 |
1,91 |
1,90 |
1,52 |
| 2,03 | 1,98 | 2,05 | 1,71 | 1,72 | 1,89 |
2,05 |
1,99 |
| 2,06 | 1,87 | 2,01 | 1,96 | 1,98 |
1,87 |
1,78 |
1,60 |
| 1,63 | 1,82 | 1,85 | 2,09 | 1,92 | 1,78 | 1,78 | 1,53 |
| 1,98 | 1,91 |
¿Cuál sería la probabilidad de que al elegir una persona al azar, ésta mida 1,81 m? ¿Y 1,73 m?
Si X es una variable aleatoria continua, la probabilidad de que tome un valor concreto es cero.
P[X = a] = 0, para cualquier valor de a.
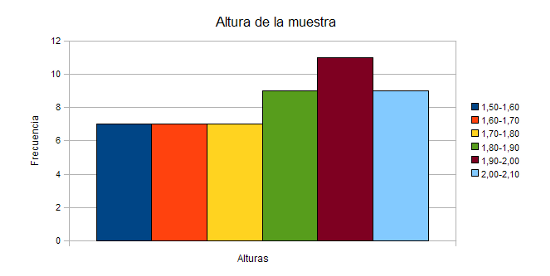 |
Si en lugar de preguntarnos por valores sueltos nos preguntamos por la probabilidad de un grupo ya la cosa cambia.
Fíjate, en la imagen de la derecha hemos agrupado los mismos datos de la tabla de arriba en intervalos de 10 centímetros de amplitud.
Ahora sin mucha dificultad, podemos calcular la probabilidad de que al elegir una persona al azar ésta esté entre 1,70 y 1,80; sería 7/50. O la probabilidad de que una persona mida menos de 1,80; sería 21/50.
Si te fijas, estas probabilidades son en realidad las frecuencias relativas, así que en lugar de este gráfico vamos a usar el de las frecuencias relativas.
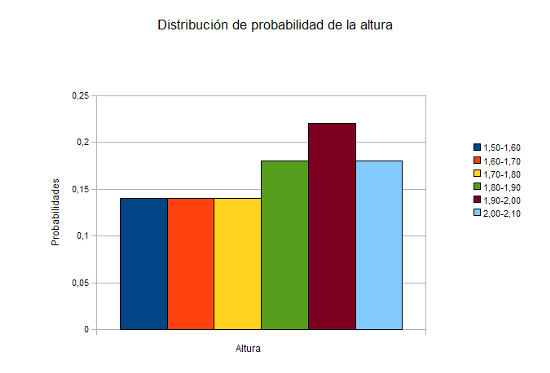 |
Pues bien, en una variable aleatoria continua, las probabilidades se calculan a través de la llamada función de densidad, función que juega un papel similar al polígono de frecuencias, y éstas se van a calcular como el área del recinto que está bajo esta curva.
En este ejemplo que estamos viendo, la función de densidad sería la función dibujada en rosa:
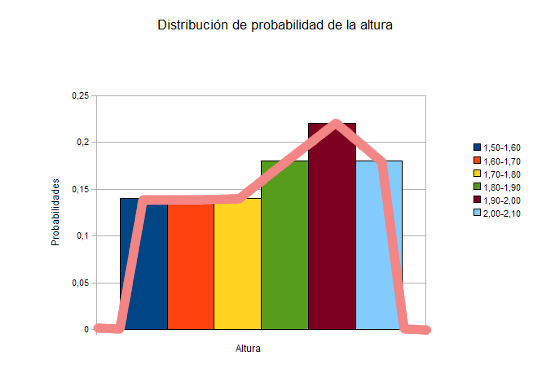 |
Aunque a decir verdad, la función de densidad es el polígono de frecuencias que surge cuando tomamos intervalos muy muy pequeñitos, es decir, con una amplitud muy pequeña. Fíjate en la siguiente escena. Pulsando sobre el botón inicio puedes ver un nuevo histograma.
Applet Descartes modificado del original de Pepe Sánchez publicado en la web Descartes bajo licencia Creative Commons.
Tenemos representado un histograma con su polígono de frecuencia. Él área bajo el histograma (azul) es 1 y como puedes ver el área bajo el polígono de frecuencia (rojo) es inferior.
Pero si aumentamos el número de intervalos, como la amplitud total es la misma, estamos haciendo que cada intervalo tenga cada vez una amplitud menor, a la vez, el polígono de frecuencias cada vez va cogiendo más forma de curva y se separa menos de los rectángulos del histograma y el área bajo éste se va acercando más a 1, llegando a coincidir si el número de intervalos es suficientemente grande.
Cuando esto ocurre, esta función dibujada en rojo es la función de densidad de esta variable aleatoria continua.
En una variable aleatoria continua, las probabilidades que calculamos están siempre asociadas a intervalos.
Si X es una variable aleatoria continua, la probabilidad de que X esté en un intervalo es el área del recinto limitado por el intervalo y la función de densidad.
En el caso de tener una variable aleatoria continua X, ya hemos visto que las probabilidades de valores concretos son 0. Así, al describir un intervalo, no influye que la desigualdad sea estricta o no para calcular la probabilidad.
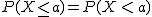

Verdadero Falso
Verdadero Falso
Verdadero Falso
Verdadero Falso
Verdadero Falso