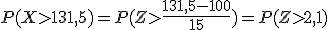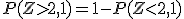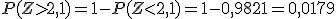3. Se ajusta como el guante a la mano
 |
| 11. Imagen de ferminet bajo licencia Creative Commons |
La distribución normal como ya hemos comentado se ajusta a un montón de situaciones y casos concretos de la naturaleza, la economía, la sociología,...
En este apartado te presentamos unas cuantas situaciones que se ajustan y se resuelven aplicando el modelo normal.
En primer lugar, en este vídeo tienes un primer ejemplo en el que la distribución normal se aplica al estudio del peso de una población:
Ejemplo o ejercicio resuelto
 |
| 12. Imagen de corazón girl bajo licencia Creative Commons |
Ahora aplicamos la distribución normal al estudio de las capacidades intelectuales, pues uno de los indicadores más fiables, el cociente intelectual se distribuye según una ley normal:
Las puntuaciones de cociente intelectual (IQ) están distribuidas normalmente con una media de 100 y una desviación típica de 15. Mensa es una organización para personas con cociente intelectual elevado y sólo acepta a personas con un IQ mayor que 131,5. Si se elige una persona al azar, ¿qué probabilidad hay de que satisfaga el requisito que exige Mensa? Si en una ciudad viven 75000 personas, ¿cuántos podrían entrar en Mensa?
Curiosidad
 |
¿Quieres saber cuál es tu cociente intelectual?
En el siguiente enlace te presentamos una página donde puedes saberlo. Tienes que realizar una serie de pruebas basadas en la lógica y la memorización y al final te derivan la puntuación obtenida a una distribución normal. Échale un poco de paciencia porque la prueba en total dura sobre 40 minutos.
Ejemplo o ejercicio resuelto
 |
| 13. Imagen de Bocadorada bajo licencia Creative Commons. |
En este ejemplo hablamos ahora de colesterol. La distribución normal tiene muchísimas aplicaciones en la medicina pues muchos indicadores se distribuyen según un modelo normal. En este ejemplo, vemos que el nivel de colesterol se distribuye según una normal.
El enunciado nos dice que una ciudad de 300.000 habitantes el nivel de colesterol en sangre sigue una distribución normal de media 192 y varianza 144. Nos pide calcular la probabilidad de que una persona elegida al azar tenga un nivel de colesterol comprendido entre 186 y 200, el número de personas con nivel de colesterol elevado, considerándose colesterol elevado si es superior a 235 y por último un nivel de colesterol de forma que el 84,2% de la población tenga un nivel superior a ese.
En la presentación que sigue se presenta la solución.
Para saber más
Como ya hemos visto, la distribución normal es una distribución de probabilidad simétrica respecto a la media, concentrando la máxima probabilidad en torno también a la media μ.
 |
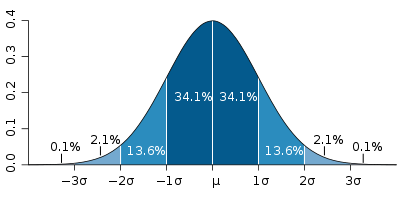| 14. Imagen en Wikimedia Commons bajo licencia Creative Commons. |
Pues bien sean cuales sean son parámetros de la distribución normal, siempre se cumple que los siguientes intervalos centrados en la media tienen las probabilidades que aparecen:
- En el intervalo [μ - σ, μ + σ] se encuentra comprendida, aproximadamente, el 68,26% de la distribución. Es decir, la probabilidad de que X pertenezca a ese intervalo es del 68,26%.
- En el intervalo [μ - 2σ, μ + 2σ] se encuentra, aproximadamente, el 95,44% de la distribución.
- Por su parte, en el intervalo [μ -3σ, μ + 3σ] se encuentra comprendida, aproximadamente, el 99,74% de la distribución.
Estas propiedades son de gran utilidad para el establecimiento de intervalos de confianza como veremos en el próximo curso. Por otra parte, el hecho de que prácticamente la totalidad de la distribución se encuentre a tres desviaciones típicas de la media justifica los límites de las tablas empleadas habitualmente en la normal estándar.
AV - Pregunta de Elección MúltipleResuelve tú ahora las siguientes cuestiones. Procede de forma similar a como lo hemos hecho en los ejemplos resuelto: en primer lugar piensa qué probabilidad hay que calcular, después tipifica y transforma la probabilidad para que puedas buscarla en la tabla.
 |
| 15. Imagen de Daquella manera bajo licencia Creative Commons |
El tiempo de vida de una bombilla sigue una distribución normal N(180, 15), donde el tiempo se mide en horas. ¿Cuál es la probabilidad de que al comprar una bombilla, luzca más de 207 horas?
|
0,8810
| |
|
0,119
| |
|
0,9641
| |
|
0,0359
|
|
0,99872
| |
|
0,99877
| |
|
0,00051
| |
|
1,00051
|