5.2. Cuando a más le corresponde menos
|
|
| 26. Fuente propia |
Un viaje a una ciudad maravillosa, con un legado arqueológico muy amplio y una gran riqueza arquitectónica. Pasear por sus calles es un placer, disfrutar de su gastronomía y del contacto con sus gentes otro tanto.
Soñar no cuesta dinero, pero viajar en la realidad sí. Si tenemos un dinero destinado a pagar el hotel o el apartamento que debemos alquilar para pasar nuestras vacaciones, los días que podamos estar dependerá del precio por día de nuestro alojamiento. Si el alojamiento es más caro nuestra estancia deberá ser más corta. Más precio menos días. Recordamos que se trata de magnitudes inversamente proporcionales.
Supón que dispones de 1000 € para destinarlo a pagar tu alojamiento, ¿cuántos días podrías conseguir si el precio es de 40 €/día?, ¿y si es de 100 €/día?
En cualquiera de sus fantásticos restaurantes y bares podemos pasar a tomar unas tapas. Mi amigo Juan dice que la ronda que pagó le salió por ..... € y que, como éramos 4, el importe medio por persona ha sido de 7,5 €. Le he tenido que corregir, en realidad estábamos 5 (tiene la costumbre de no contarse a sí mismo). Luego, la consumición por persona ha salido por .... (¿más?, ¿menos?, ¿cuál fue el importe total?). Sin duda tienes la respuesta. Claro, más consumidores para un mismo total, tocan a menos precio por persona (a 6 €) y, por supuesto, la consumición salió por 30 €.
SOBRE CUÁNTO CORRESPONDE Y CÓMO REPARTIMOS.
Intentaremos en este apartado que domines los contenidos básicos relacionados con la proporcionalidad inversa y los repartos inversamente proporcionales. Repasaremos el concepto visto en el punto 5 y trabajaremos la resolución de problemas de proporcionalidad inversa y repartos inversamente proporcionales.
Vamos a resolver estas actividades utilizando el procedimiento que podríamos llamar de reducción a la unidad, en el que calcularemos el valor de la segunda magnitud que corresponde al valor 1 de la primera magnitud. Este valor que calculamos es lo que hemos llamado antes constante de proporcionalidad inversa.
Con esta primera escena se podrán resolver actividades de magnitudes inversamente proporcionales de forma ordenada sin la utilización de números decimales. La escena indica los pasos a seguir para su resolución.
Repartos inversamente proporcionales
Consiste en repartir una cantidad entre varias partes de forma que lo que reciba cada una de las partes sea inversamente proporcional a la cantidad aportada por cada una.
Para hacer un reparto inversamente proporcional entre varias partes, se hace un reparto directamente proporcional entre los inversos de cada una de las partes.
Con la siguiente escena se pueden hacer, paso a paso, repartos inversamente proporcionales desde dos a cinco partes.
|
María recibirá 89 €, Jesús, 133 € y Francisco, 311 €.
| |
|
Todos deben recibir lo mismo.
| |
|
María recibirá 273 €, Jesús, 182 y Francisco, 78.
| |
|
A María le corresponderán 300 €, Jesús, 200 € y a Francisco, 33 €. |
|
La sucursal A recibirá 483.876 €, la B, 604.845 € y la C, 161.292 €.
| |
|
La sucursal A recibirá 260.419,38 €, la B 208.335,5 € y la C, 781.258,13 €.
| |
|
Cada una de las tres sucursales recibe 416.671 €-
| |
|
Ninguna de las anteriores es correcta.
|
|
Aproximadamente 33, pero no da exacto.
| |
|
600 €.
| |
|
12 unidades.
| |
|
La misma cantidad, basta poner más dinero.
|
|
6 horas.
| |
|
1,5 horas.
| |
|
24 horas.
| |
|
Depende del tiempo del tiempo. Si llueve no pueden pintar.
|

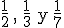 y hacemos su suma obteniendo
y hacemos su suma obteniendo 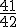 . El valor de la suma es el total de los inversos y hacemos un reparto directamente proporcional de los 533 € respecto de ese total.
. El valor de la suma es el total de los inversos y hacemos un reparto directamente proporcional de los 533 € respecto de ese total.
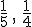 y
y 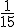 y hacemos su suma obteniendo
y hacemos su suma obteniendo 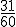 . El valor de la suma es el total de los inversos y hacemos un reparto
directamente proporcional de 1.250.013 € respecto de ese total.
. El valor de la suma es el total de los inversos y hacemos un reparto
directamente proporcional de 1.250.013 € respecto de ese total.