2.1. Campana sobre campana.
El título de este apartado es la letra de un famoso villancico popular navideño, pero no nos estamos refiriendo a él. Nos estamos refiriendo a la forma tan curiosa que tiene la función de densidad de una distribución normal.
¿A la forma? Sí, a la silueta que obtenemos cuando representamos la gráfica de esta función. Ya verás ...
 |
| The Chasm - Roger Moore, imagen de Luc Galoppin con licencia by-2.0-deed |
A continuación comenzamos el análisis detallado de la distribución normal.
Diremos que una variable aleatoria continua X, sigue una distribución normal de media, μ, y desviación típica, σ, y lo representaremos: X es N(μ,σ), si cumple que su función de densidad viene dada por la siguiente expresión:
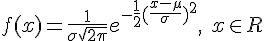
Si representamos esta función, nos saldrá algo parecido a lo que se muestra en la siguiente imagen:
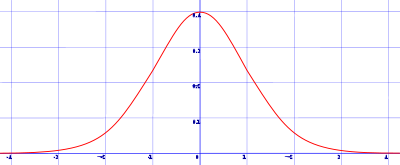
Como ves, con forma de campana.
Ya sé lo que estás pensando: ¡madre mía, qué función! ¿y ésta es la distribución normal? Pues entonces, la que no sea normal, ¿cómo será?
No te preocupes que no pasa nada. No necesitarás trabajar con esta función para calcular las probabilidades.
Ya hemos comentado, en el apartado anterior, que en las variables aleatorias continuas, la probabilidad de un intervalo es igual al área de la región encerrada entre la porción de gráfica de la función de densidad en ese intervalo y el eje OX. Pero, para calcular ese área, necesitamos usar el concepto de integral (que se estudiará en 2º de Bachillerato).
¿Qué haremos entonces si no sabemos trabajar con integrales? Usaremos caminos alternativos para calcular probabilidades con estas distribuciones (pero realmente, detrás de todo, están las integrales).
En el siguiente applet de Geogebra podrás practicar de un modo más ameno y sencillo (éste es uno de los caminos alternativos comentados).
Funcionamiento del applet.
Deberás modificar los valores de la media (μ) y la desviación típica (σ) y, automáticamente, aparecerá representada la función de densidad de la distribución N(μ,σ). Después, desplazando los puntos A y B, aparecerá coloreada la región encerrada entre dicha gráfica y el eje OX, así como el valor del área de dicha región, que será el valor de la probabilidad de la variable N(μ,σ) en el segmento AB.
Ayúdate del applet anterior, para contestar a las siguientes cuestiones:
1) Describe brevemente el efecto que produce sobre la función de densidad aumentar (disminuir) el valor de la media (μ)
2) Describe brevemente el efecto que produce sobre la función de densidad aumentar (disminuir) el valor de la desviación típica (σ)
3) Si X ~ N(0,1), calcula P(1<X<2,25).
4) Si X ~ N(0,1), calcula P(X=-0,5) (Coloca A y B juntos)
¿Qué observas?
5) Si X ~ N(0,1), calcula P(X ≥ -1) (Coloca A sobre -1 y B en cualquier lugar mayor que 4, sobre la flecha podría valer)
6) Si X ~ N(2;0,8), calcula P(-2<X<2)
7) Si X ~ N(-0,5;1,5), calcula P(-2<X<2)
8) Si X ~ N(4,7;1,2), calcula P(X<2) (Coloca B sobre 2 y A en cualquier lugar menor que -1)
9) Si X ~ N(-3;1,3), calcula P(X>-5) (Coloca A sobre -5 y B en cualquier lugar mayor que 4, sobre la flecha podría valer)
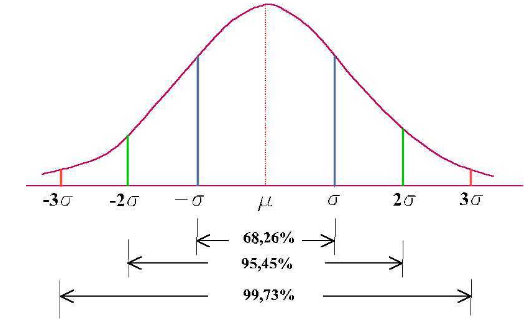 |
| Intervalos característicos en una distribución normal |
Vamos a describir algunas características de una distribución N(μ,σ). Basta mirar con detenimiento la gráfica de su función de densidad, para observar que:
a) Es simétrica respecto de la media, es decir, la media divide la gráfica en dos partes iguales.
b) Es creciente hasta que x=μ y decreciente a partir de él. En x=μ la función de densidad alcanza su máximo.
Además, sea cuales sean los valores de μ y σ, siempre se cumple lo siguiente:
c) En el intervalo (μ-σ , μ+σ) se encuentra el 68,26 % de los datos.
d) En el intervalo (μ-2σ , μ+2σ) se encuentra el 95,45 % de los datos.
e) En el intervalo (μ-3σ , μ+3σ) se encuentra el 99,73 % de los datos.
Elige un valor concreto para μ y otro para σ y, con ayuda del applet de Geogebra, comprueba que se cumple lo que se afirma acerca de los tres intervalos característicos.
Con el applet de Geogebra muy bien, ¿verdad? Pero, el applet está limitado. Por ejemplo, no podemos ponerle valores de σ mayores de 5. Y no sólo eso, ¿y si no tienes applet? ¿cómo calcularás una probabilidad en una distribución normal?
No pasa nada, los matemáticos tienen soluciones para todo.