1. Juntitos, juntitos, no aislados.
Si haces un poco de memoria, recordarás cómo, en el tema anterior, clasificamos las variables aleatorias en dos grandes grupos: variables aleatorias discretas y variables aleatorias continuas
Las variables discretas eran las que tomaban valores aislados mientras que las continuas eran las que podían tomar cualquier valor entre dos concretos, es decir, puede tomar valores "tan juntitos" como queramos.
Ejemplo de variable discreta: Si lanzamos un dado normal de 6 caras y miramos el resultado obtenido sólo puede tomar los valores: 1,2,3,4,5 y 6 (valores aislados).
Ejemplo de variable continua: Si observamos los datos de velocidad (en km/h) de los vehículos que pasan por un radar fijo colocado en una autopista durante un fin de semana, comprobaremos que tenemos muchísimos valores distintos. (120,1 117,8 114,3 114,31 112,9 ...) (valores continuos, algunos casi idénticos).
Al igual que ocurre siempre con las matemáticas, situaciones como ésta hacen que sea necesario "inventar" otro objeto matemático nuevo, en este caso, otro tipo de variables aleatorias, puesto que las variables discretas no nos permiten manejar situaciones como la comentada del radar. Estas nuevas variables seran las variables aleatorias continuas.
Diremos que una variable aleatoria es continua si al realizar el experimento aleatorio, entre cada dos valores de la misma, el número de valores (de resultados posibles) que puede tomar es infinito.
Por ejemplo, el nivel de colesterol en sangre de un conjunto de personas, calificaciones obtenidas por los participantes en un concurso oposición o el peso de los habitantes de un país.

|
| Imagen de Autoescuela Miguel con licencia by-2.0-deed |
Vamos a suponer que hemos recogido, en una tabla, las velocidades (en km/h) de 40 vehículos que han pasado por delante de un rádar ubicado en una autopista, durante un periodo de tiempo de media hora.
| 120,1 | 117,8 | 114,3 | 114,31 | 112,9 |
124,2 | 110 |
116,6 |
| 119,7 | 106,7 | 102,1 | 102,2 | 116,2 |
116,7 |
111,9 |
111,52 |
| 120,3 | 119,8 | 120,5 | 107,1 | 117,2 | 118,9 |
101,5 |
119,9 |
| 112,06 | 118,7 | 120,1 | 119,6 | 109,4 |
114,4 |
101,75 |
106 |
| 116,79 | 118,2 | 128,5 | 120,95 | 119,9 | 129,8 | 113,8 | 111,52 |
¿Cuál sería la probabilidad de que al elegir la velocidad de un vehículo al azar, ésta fuese igual a 105 km/h? ¿Y que fuese igual a 120,8 km/h?
Si X es una variable aleatoria continua, entonces, la probabilidad de que tome un valor concreto es cero (probabilidad nula).
P[X=a] = 0, para cualquier valor de a.
 |
Ya hemos visto, que es muy difícil encontrar, en una toma datos, un valor que sea idéntico a uno propuesto por nosotros.
Pero, ¿y si en lugar de preguntarnos por un valor suelto (aislado), nos preguntamos por la probabilidad de que ocurra un grupo (intervalo) de valores?
Pues la respuesta es que la situación cambia bastante. Vamos a verlo:
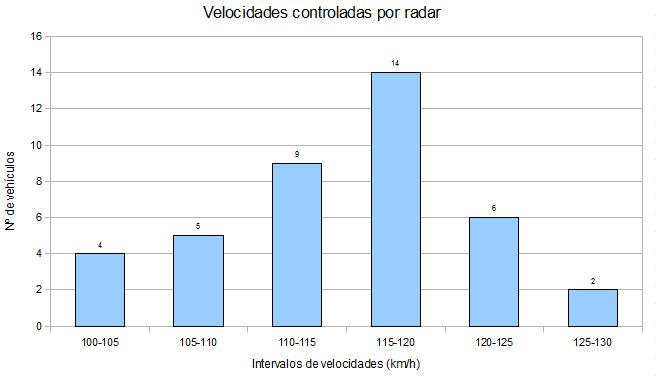
Observa con detenimiento el diagrama de barras representado a la derecha.
Lo que hemos hecho es agrupar los datos de la tabla anterior en 4 intervalos de 5 km/h de amplitud, contar cuántas velocidades caen en cada uno de ellos y, finalmente, representarlos.
Gracias a esta representación, es bastante sencillo, por ejemplo, responder a cuestiones del tipo:
a) Obtener la probabilidad de que al elegir una velocidad al azar, ésta se encuentre entre 110 y 115 km/h.
Basta con mirar el histograma, para responder que, la probabilidad pedida es 9/40.
b) Calcular la probabilidad de que una velocidad, tomada al azar, sea menor o igual que 120 km/h.
De la forma que tiene el histograma, deducimos que la probabilidad pedida es 32/40.
¿Fácil, verdad?
Pues demos un paso más hacia adelante. Como habrás observado, estas probabilidades obtenidas no son más que las frecuencias relativas, así que en lugar de usar el gráfico anterior, vamos a fijarnos ahora en el de frecuencias relativas (probabilidad).
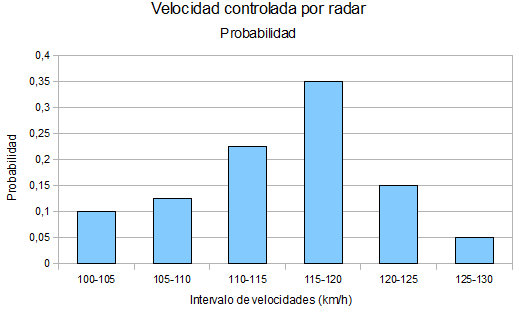 |
Pues bien, en una variable aleatoria continua, para calcular probabilidades necesitamos una función que llamaremos función de densidad de la variable. Esta función, tiene un papel similar al polígono de frecuencias.
Gracias a ella, las probabilidades en una variable aleatoria continua se calculararán obteniendo cuánto vale el área del recinto que queda bajo esta función y el eje OX.
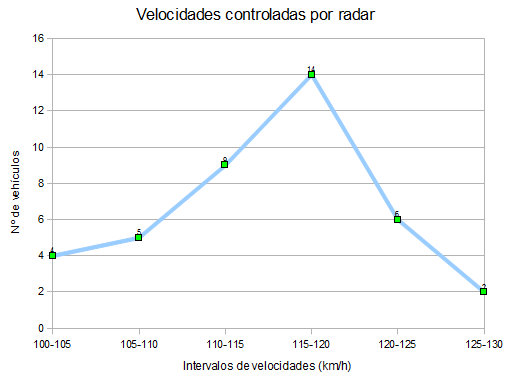
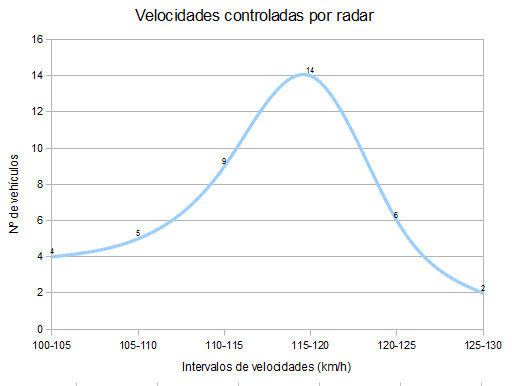
En las siguientes imágenes vemos:
- En la izquierda, está representada la función de densidad de nuestra variable. Simplemente, lo que se hemos hecho es construir el polígono de frecuencias a partir del diagrama de barras mostrado anteriormente.
- A la derecha, se ha "suavizado" el polígono de frecuencias de la imagen anterior. Hemos tomado intervalos "muy pequeñitos de velocidad" (puntos, muy juntitos), lo que ha permitido corregir "los picos" y ¡¡sorpresa!!, ¿qué obtenemos? Efectivamente, una campana. Pues ésta realmente es la verdadera función de densidad de nuestra variable.
 |
 |
En la siguiente escena de Descartes, se muestra de una manera muy gráfica, el paso del polígono de frecuencias a la función de densidad.
Pulsa el botón Inicio para comenzar un ejemplo nuevo. Se cargará un nuevo histograma de frecuencias.
|
|
| Escena del Proyecto Descartes. Modificada de la original de Pepe Sánchez con licencia Creative Commons. |
Interpretación de la escena: ¿Cómo obtener la función de densidad a partir del histograma de frecuencias?
En la escena aparece representado un histograma con su polígono de frecuencias correspondiente. El área bajo el histograma (azul) vale 1 y como puedes comprobar el área bajo el polígono de frecuencias (rojo) es inferior a 1, estamos desaprovechando espacio. Pues la idea es precisamente esa, rellenar el hueco que queda vacío.
Para ello, iremos aumentando el número de intervalos ("nº interv"). Entonces, como la amplitud total es fija, lo que en realidad estamos haciendo es que cada intervalo tenga cada vez una amplitud menor. Al mismo tiempo que aumentamos el número de intervalos, el polígono de frecuencias cada vez va cogiendo más forma de curva, separándose menos de los rectángulos del histograma original y al mismo tiempo, el área bajo el histograma se va acercando cada vez más a 1, llegando a valer exactamente 1 si el número de intervalos es lo suficientemente grande.
Cuando ésto ocurre, ésto es, cuando ambos coinciden y sus áreas valen 1, la función dibujada en rojo es la función de densidad de esta variable aleatoria continua.
Si tenemos una variable aleatoria continua, X, entonces recordamos que:
a) 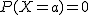
En una variable aleatoria continua, lo que realmente tiene sentido y es interesante es calcular las probabilidades de que un valor se encuentre en un cierto intervalo.
b) 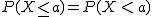
c) 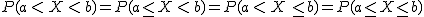
Si X es una variable aleatoria continua, la probabilidad de que X esté en un cierto intervalo se calcula como el área del recinto limitado por dicho intervalo y la gráfica de la función de densidad. Da igual que sea intervalo cerrado, abierto o semi-abierto, porque las probabilidades en los extremos valen cero (P(X=a)=P(X=b)=0) y no aportan nada.
Ha llegado el momento de que pongas a prueba lo que has aprendido sobre las variables aleatorias continuas.
Para ello, selecciona Verdadero o Falso en cada una de las siguientes cuestiones:
Si X es una variable aleatoria continua, entonces:
Verdadero Falso
Verdadero Falso
Verdadero Falso
Verdadero Falso
Verdadero Falso