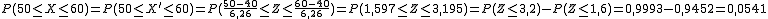4. Mientras más datos, mejor.
 |
| Imagen de Jorge Franganillo con licencia by-2.0-deed |
En el tema anterior, parte de nuestro esfuerzo se dedicó a trabajar con las distribuciones binomiales. Este tipo de distribuciones nos permitían obtener la probabilidad de obtener k éxitos al realizar n veces un experimento.
Vamos a recordar un ejemplo de aplicación de la binomial.
Seguro que, alguna vez, has realizado un examen tipo test sin estudiar, bueno, o no habiendo estudiado mucho. Piensa en un examen tipo test compuesto por 100 preguntas, con dos opciones Verdadero o Falso en cada una de ellas, en el que se aprueba acertando, al menos, 85. ¿Qué probabilidad tendrías de aprobar un examen como éste respondiendo al azar todas las preguntas?
Si analizamos el resultado, vemos claramente que este problema se resuelve mediante una distribución binomial.
Aparecen: éxitos, acertar preguntas; fracasos, fallar en las preguntas; el experimento, "acertar una pregunta"; se realiza n=100 veces, de manera independiente ya que acertar una pregunta es independiente de la anterior.
Por tanto, tenemos una binomial con n = 100 y p, probabilidad de éxito en una pregunta vale 0,5.
Entonces, la variable X que estudia el "número de aciertos en 100 preguntas", se distribuye según una B(100; 0,5)
¿Pero cómo calculábamos las distintas probabilidades de una distribución de ese tipo? Era necesario trabajar con los poco amigables binomios porque la fórmula de la probabilidad en las binomiales era:
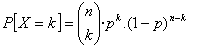
Esta fórmula era un poco pesada de aplicar y si teníamos que calcular la probabilidad de que X fuese mayor o menor que un cierto valor, como es nuestro caso, había que aplicarla varias veces. En nuestro ejemplo sabemos que se aprueba si X=85, o X=86, .... o X=100. Es decir, tendríamos que aplicar la fórmula y sumar desde X=85 hasta X=100. No te asustes, para eso está la normal que, cual Superman de las distribuciones, acudirá en nuestra ayuda.
Lo que ocurre es que si tenemos muchos datos, la distribución binomial, se aproxima mucho, mucho, a una distribución normal y, ya hemos visto que trabajar con distribuciones normales es mucho más facil, que trabajar con binomiales. De ahí la importancia del siguiente resultado:
Teorema de De Moivre - Laplace
Si tenemos que X es una variable aleatoria binomial de parámetros n y p, X ~ B(n,p), entonces X se puede aproximar a una distribución normal de media μ=n·p y desviación típica σ=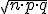 (donde q=1-p) si se cumplen las dos condiciones siguientes:
(donde q=1-p) si se cumplen las dos condiciones siguientes:
(Condición 1) n ≥ 30
(Condición 2) n·p ≥ 5 y n·q ≥ 5
Entonces, la variable binomial X ~ B(n,p) quedaría aproximada por la variable normal X ~ N(np,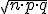 ).
).
 |
| Imagen de sergis blog con licencia by-2.0-deed |
Vamos a calcular la probabilidad que tendrías de aprobar un examen como el indicado en el ejemplo anterior, respondiendo a las preguntas "al tun-tun", es decir, de manera aleatoria.
Recordemos las características del examen:
El examen consta de 100 preguntas, con dos opciones Verdadero o Falso en cada una de ellas, en el que se aprueba acertando al menos 85.
¿Qué probabilidad tendrías de aprobar?
 |
| This is the madness! Imagen de alt1040 con licencia by-sa-2.0-deed |
Una compañía multinacional dedicada a la fabricación de teléfonos móviles ha estimado que el 2% de las móviles que producen tienen defectos de fabricación. La semana pasada, una franquicia dedicada a la venta de teléfonos móviles realizó un pedido de 2000 teléfonos.
Vamos a dar un repaso global a distintas cuestiones sobre las variables aleatorias a través de este problema. Para ello, debes realizar los pasos que sea necesario con bolígrafo y papel y, posteriormente, seleccionar una de las opciones que se presentan en cada una de las cuestiones:
(1) La variable aleatoria que tenemos que definir es:
|
X = "El móvil tiene defectos de fabricación"
| |
|
X = "Tamaño del móvil"
|
|
p=0,2 y q=0,8
| |
|
p=0,02 y q=0,98
| |
|
0,5
|
|
No se puede aproximar.
| |
|
Sí se puede aproximar (porque se cumplen las condiciones del Teorema de De Moivre-Laplace) y la aproximación es N(40; 8,35)
| |
|
Sí se puede aproximar (porque se cumplen las condiciones del Teorema de De Moivre-Laplace) y la aproximación es N(40; 6,26)
|
|
P(X < 60)
| |
|
P(X = 60)
| |
|
P(X ≤ 60)
| |
|
P( X ≥ 60)
|
|
0,99
| |
|
53'14
| |
|
0,054
|
Sabemos que en las distribuciones discretas el objetivo es calcular P[X=a] con a un valor concreto.
También sabemos que en las distribuciones continuas lo que tiene sentido es calcular P[a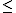 X
X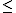 b],
es decir, probabilidades en intervalos, ya que, en este tipo de
distribuciones, las probabilidades en valores concretos valen 0, es
decir, P[X=a]=0
b],
es decir, probabilidades en intervalos, ya que, en este tipo de
distribuciones, las probabilidades en valores concretos valen 0, es
decir, P[X=a]=0
Pero entonces, ¿qué ocurre cuando aproximamos una distribución binomial (discreta), X, por una distribución normal (continua), X' y queremos calcular P[X=a] con a un valor concreto?
De este problema se ocupó el matemático inglés Frank Yates (1902-1994) y propuso una manera de solucionarlo que se conoce con el nombre de corrección de Yates, la cual se muestra a continuación:
La aproximación de una variable discreta X por una continua a la que llamaremos X', genera un cierto error que se corrige modificando el intervalo cuya probabilidad se quiere calcular. Estas son situaciones y correcciones posibles:
P(X = a) = P( a - 0,5 ≤ X' ≤ a + 0,5)
P(X ≤ a) = P( X' ≤ a + 0,5)
P(X < a) = P( X' ≤ a - 0,5)
P(X > a) = P( X' ≥ a + 0,5)
P(X ≥ a) = P( X' ≥ a - 0,5)
En el siguiente enlace accederás a la página de Vitutor donde podrás repasar, consolidar y ampliar los contenidos de la distribución normal y sobre la aproximación de la binomial por una normal.
La página contiene resumen de los conceptos y fórmulas más importante, así como ejercicios y problemas resueltos.
Si necesitas la tabla de la N(0,1) en esta página de Vitutor puedes encontrarla tambien, para que elijas la que más te guste de entre todas las presentadas a lo largo del tema.
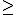 85 (debes acertar 85 preguntas o más).
85 (debes acertar 85 preguntas o más).
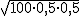 , es decir,
, es decir,
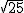 ) → X ~ N(50;5)
) → X ~ N(50;5)
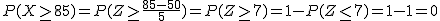

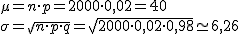
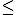 X
X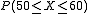
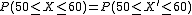
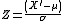 y entonces,
y entonces,