1.3. Coeficiente de reducción
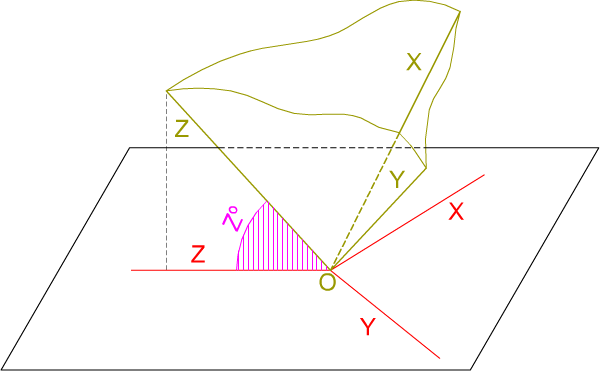
En el sistema diédrico vimos que cuando una recta es paralela a un plano de proyección al proyectarla sobre dicho plano obtenemos su verdadera magnitud; si la recta es oblicua las proyecciones tienen una longitud menor a la real, es decir, su magnitud queda reducida.
En el sistema axonométrico una longitud contenida en los ejes axonométricos, proyectada sobre el plano del cuadro, sufre una determinada reducción en cada eje.
Esta reducción viene determinada por el coeficiente de reducción, que es la relación entre la medida real de un segmento situado en el espacio y la de su proyección sobre el plano del cuadro.
Para poder representar cualquier magnitud real, necesitaremos conocer la escala proyectiva, llamada escala axonométrica, que se calcula para cada eje axonométrico, según el ángulo que este forme con el plano del cuadro.
Esta escala gráfica se obtiene multiplicando el valor de la unidad real por el coeficiente de reducción correspondiente.
El valor del coeficiente de reducción depende de la magnitud del ángulo que forma cada eje con el plano del cuadro.
En las axonometrías oblicuas, al estar una de las caras del triedro trirrectángulo contenida en el plano del cuadro, todo segmento contenido, o paralelo, a dicha cara, se proyectará en verdadera magnitud. Por tanto, solamente se le aplicará el coeficiente de reducción a un eje.
- Matemático. Mediante el coseno del ángulo que forma cada eje con el plano del cuadro.
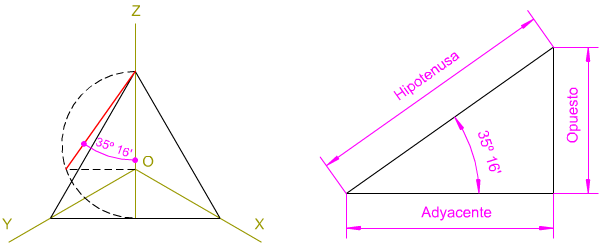
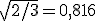
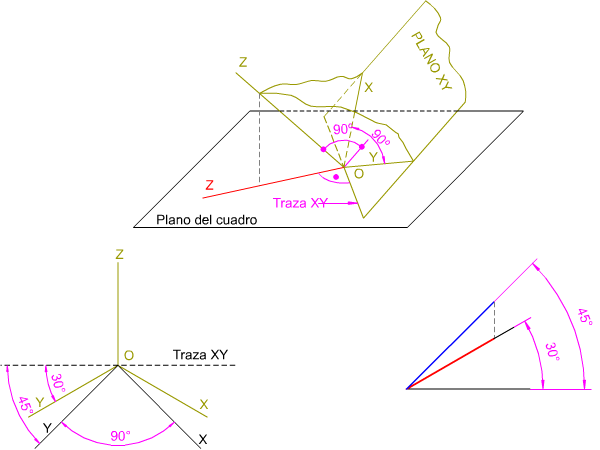
- Gráfico. La intersección (traza ordinaria) de una cara del triedro, con el plano del cuadro, forma 90º con la arista de la otra cara. Al abatir dicha cara, esta formará con su traza 45º.
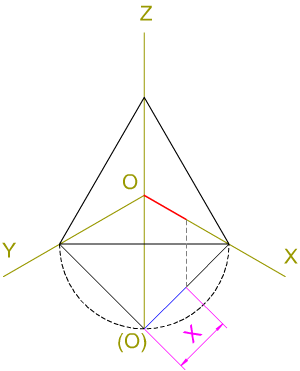
En la imagen inferior, en perspectiva isométrica, puedes ver cómo la traza de la cara XY del triedro, con el plano del cuadro, forma 90º con el eje Z. La cara XY abatida forma 45º con la traza XY; así mismo el eje Y forma 30º con dicha traza. Recuerda que las aristas del triedro (ejes de la isometría) se cortan ortogonalmente dos a dos.
Podemos simplificar todo lo anterior construyendo dos semirrectas que formen 45º y 30º respectivamente con una horizontal. Toda magnitud real colocada sobre la semirrecta del ángulo de 45º al proyectarse sobre el lado del ángulo de 30º quedará reducida según el coeficiente 0,816.
 Existe otro método gráfico, que permite un trazado más preciso; abatir el triángulo fundamental de las trazas, mencionado en el apartado anterior. Este recurso gráfico lo veremos en el siguiente curso.
Existe otro método gráfico, que permite un trazado más preciso; abatir el triángulo fundamental de las trazas, mencionado en el apartado anterior. Este recurso gráfico lo veremos en el siguiente curso.
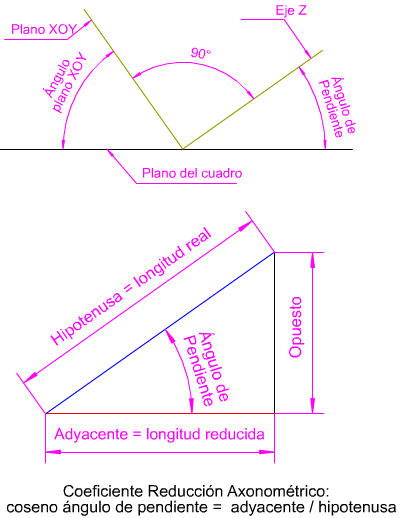
En la imagen izquierda tienes la demostración gráfica de la reducción de una magnitud real aplicando el coseno del ángulo de pendiente (el que forma cada eje axonométrico con el plano del cuadro).
Con la siguiente aplicación, cortesía de Juan José Romero Anaya (juanjoseromero@tekisuto.es), puedes calcular la reducción de una longitud real según el ángulo de pendiente.
Como ejemplo comprueba la reducción isométrica de distintas longitudes; recuerda que el coeficiente de reducción para este tipo de axonometría es de 0,816 y que su ángulo de pendiente (35º 16' en sexagesimal) debes pasarlo al sistema mixto: 35.26º.
Introduce la longitud real:
Introduce el ángulo de pendiente (sin º):
Longitud reducida: