2.5. Triángulo escaleno. Construcción
Para la construcción de un triángulo escaleno se necesitan tres datos que guarden relación entre sí:
- Un lado, su altura y su ángulo opuesto
- Un lado, su mediana y la mediana de uno de los lados adyacentes.
- Dos lados y el radio de la circunferencia circunscrita.
- Un lado, un ángulo adyacente y el radio de la circunferencia inscrita,
- Etc.
CONSTRUCCIÓN:
Método Directo:
- Conocido un lado (a) en verdadera magnitud y posición y la longitud de los otros dos (b y c): para resolver este ejercicio tienes que tener en cuenta la disposición de los lados (sentido contrario a las agujas del reloj)
- Dado un lado (a) en verdadera magnitud y posición, la longitud de otro lado (b) y el ángulo que ambos forman (Cº): tienes que construir un ángulo (Cº) de lados conocida su magnitud.
- Dada la altura de un lado (ha) en verdadera magnitud y posición y las longitudes de los otros dos lados (b y c): recuerda que la altura es un segmento perpendicular a su lado opuesto (y viceversa) por tanto, tienes que trazar una recta perpendicular a la altura dada.
Método de los lugares geométricos:
- Conocido un lado (a) en verdadera magnitud y posición, su ángulo opuesto (Aº) y la longitud de otro lado (b o c): para resolver este ejercicio tienes que recurrir al trazado del arco capaz del ángulo opuesto del lado dado.
- Dada la suma de dos lados (a + b) en verdadera magnitud y posición, el ángulo que ambos forman (Cº) y la longitud del tercer lado (c): tienes que aplicar los conceptos y procedimientos explicados en la animación del apartado 2.2.
- Conocido un lado (a) en verdadera magnitud y posición, el radio de la circunferencia circunscrita y la longitud de otro lado (b o c): recuerda que la circunferencia circunscrita es el arco capaz de todos los lados del triángulo, por tanto ,el radio dado y la mediatriz del lado dado (a) determinarán el circuncentro.
- Dado un lado (a) en verdadera magnitud y posición, uno de los ángulos adyacentes (Bº o Cº) y el radio de la circunferencia inscrita: en los triángulos escalenos los puntos de contacto (tangencia) de los lados con la circunferencia inscrita están situados a la misma distancia respecto de cada vértice.
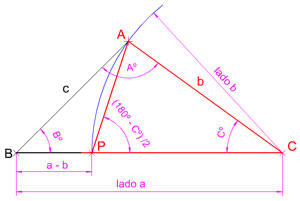 Si al lado mayor de un triángulo isósceles o escaleno le restamos otro de sus lados obtenemos un triángulo isósceles.
Si al lado mayor de un triángulo isósceles o escaleno le restamos otro de sus lados obtenemos un triángulo isósceles.
En la imagen izquierda puedes observar como en un triángulo escaleno al restar el lado menor b a su lado mayor a quedan determinados dos triángulos:
- Isósceles (ACP) lados: base AP y lados iguales b (AC) y CP.
- Escaleno (BAP) lados: lado c, diferencia lados ab (BP) y CP.
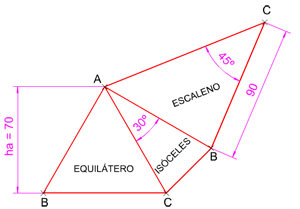 Realiza la composición poligonal de la imagen izquierda según los siguientes datos dados en milímetros:
Realiza la composición poligonal de la imagen izquierda según los siguientes datos dados en milímetros:
- Triángulo equilátero: conocida su altura ha = 70.
- Triángulo isósceles: conocido el ángulo opuesto a la base Aº = 30º y uno de los lados iguales b = lado del triángulo equilátero anterior.
- Triángulo escaleno: conocido el lado c = lado del triángulo isósceles anterior, su ángulo opuesto Cº = 45º y el lado b= 90.
¿Necesitas ayuda para resolver este ejercicio?