3. Cuadriláteros

Como forma geométrica los cuadriláteros son fundamentales en el diseño y en el arte:
- En los mosaicos romanos, bizantinos y árabes.
- En el arte abstracto numerosos artistas han empleado la abstracción geométrica para transmitir sus sentimientos. A partir de las formas geométricas básicas (círculo, triángulo y cuadrado) se desarrollan el resto de las formas.
- En el Op Art (arte óptico) el uso de la geometría y sus formas elementales genera sensaciones de tridimensionalidad, movimiento y vibración.
- En las culturas precolombinas los artistas para decorar sus obras usaron, entre otras formas geométricas, los cuadriláteros, concretamente paralelogramos basados en rombos y cuadrados.
En la fotografía superior puedes ver un fragmento de un mosaico expuesto en el Museo de Arte Romano de Mérida.
Los cuadriláteros engloban varias figuras de formas distintas: paralelogramos, trapecios y trapezoides; pero de igual estructura: todos ellos se componen de dos triángulos interiores de lado común una de las diagonales
Esta característica esencial es la que vamos a emplear en la construcción de estos polígonos.
Los hindúes tenían conocimientos avanzados en geometría: el trazado de cuadrados, rectángulos, triángulos, círculos, conos, cilindros, etc.; además podían calcular áreas, dividir segmentos en partes iguales o proporcionales.
También sabían calcular el área de figuras poligonales y el volumen de la pirámide y del tronco de pirámide, usando una medida aproximada al número 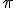 .
.
Todos estos conocimientos constituyen la geometría védica y han llegado a nosotros a través de las escrituras religiosas, como los Veda y el Sura-Sutra o reglas de cuerda.