1.2. Máximos y mínimos... a trocitos.
En ocasiones un suceso viene expresado por lo que en otros temas hemos llamado una función definida a trozos. Para este tipo de funciones, debemos analizar también los puntos donde cambia la definición de la función y por otra parte, verificar si los puntos donde la derivada se anula pertenecen al dominio de definición respectivo.
Así, nos podemos encontrar, por ejemplo, con el estudio de una función que nos indique la población de un determinado insecto en una determinada localidad (x medida en años y f(x) en miles de unidades) al lanzar ciertos productos químicos, y su aumento en el momento de reinsertar la especie en el ecosistema al desaparecer al cabo de un año.
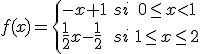
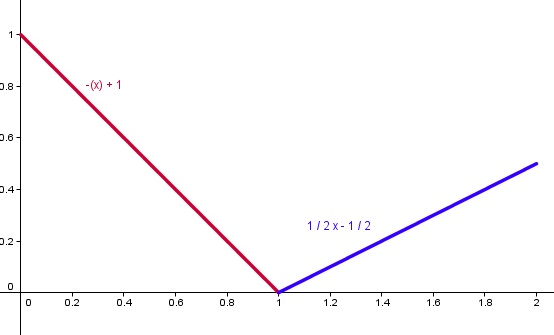
La derivada de la función indicada es
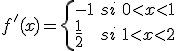
por lo que la derivada no se anula nunca. Sin embargo, al observar la gráfica de la función f, observamos que el máximo lo alcanzamos en uno de los puntos extremos del intervalo de definición y el mínimo en el punto donde cambia la definición de la función. El máximo lo alcanzamos para x=0, f(0) = 1 y el mínimo para f(1) = 0.
|
|
| Fuente propia |
Anabel ha comprado un movil nuevo, última generación, y quiere probar todas las utilidades que trae éste. Ya ha probado la cámara de fotos, el reproductor de música y ahora quiere probar el gps. El móvil tiene una aplicación que le indica la distancia a la que se encuentra de su casa en cada momento y al final del paseo, le presenta una gráfica que le indica el tiempo transcurrido y la distancia a ésta (en cientos de metros).La función que indica esta distancia es
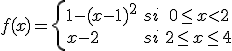
A Anabel le ha encantado su nueva aplicación de gps en el móvil y vuelve a dar un paseo para comprobar su efectividad. En la anterior ocasión, volvió a casa y la aplicación lo detectó sin problema. En esta ocasión no vuelve a casa , se aleja constantemente, a diferentes velocidades. Indica el punto de mayor distancia que ha alcanzado Anabel si la función es la siguiente:
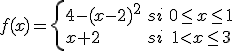

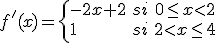
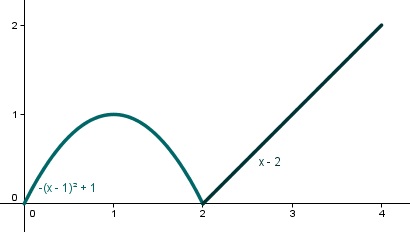 Veamos
ahora los valores de las función f en los valores críticos, es decir,
en los puntos donde la función se anula, los puntos donde cambia la
definición de la función y los extremos del intervalo donde f está
definida.
Veamos
ahora los valores de las función f en los valores críticos, es decir,
en los puntos donde la función se anula, los puntos donde cambia la
definición de la función y los extremos del intervalo donde f está
definida.