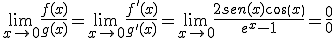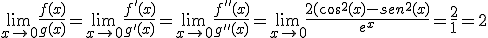4. Especial Selectividad
Se desea construir una lata de conserva en forma de cilindro circular recto que tenga una superficie total de 200 cm2. Determina el radio de la base y la altura de la lata para que el volumen sea máximo
Determina dos números reales positivos sabiendo que su suma es 10 y que el producto de sus cuadrados es máximo.
Solución: Un número es
y el otro es
.
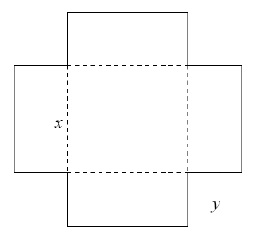
Hallar las dimensiones de un depósito abierto superiormente, en forma de prisma recto de base cuadrada, de 50 m3 de volumen, que tenga superficie mínima.
La potencia f(x) en watios consumida por cierto aparato eléctrico, en función de su resistencia (x) en ohmios viene dada por la expresión:
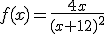
Hallar la potencia máxima y el correspondiente valor de x.
De todos los triángulos rectángulos cuyos catetos suman 15 cm, halla el que tiene área máxima
El área máxima es
cm3
Calcular el siguiente límite:
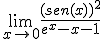
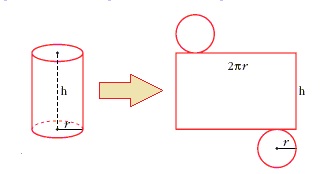 La expresión que proporciona el área de un cilindro es
La expresión que proporciona el área de un cilindro es
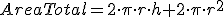
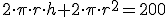 . Simplificando
. Simplificando 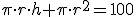 y despejando la altura
y despejando la altura
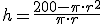
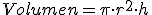 , por lo que sustituimos h en esta expresión y obtenemos una nueva función de volumen en una nueva variable ,
, por lo que sustituimos h en esta expresión y obtenemos una nueva función de volumen en una nueva variable , 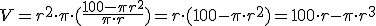
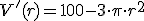 e igualando a 0, se consigue la ecuación
e igualando a 0, se consigue la ecuación 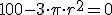 , con solución
, con solución 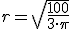 .
.
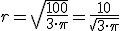 , sustitumos en la expresión que proporciona la altura y calculamos h,
, sustitumos en la expresión que proporciona la altura y calculamos h, 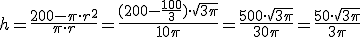
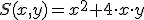 , donde x representa el lado del cuadrado que forma la base y la y la altura.
, donde x representa el lado del cuadrado que forma la base y la y la altura.
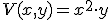 y el enunciado nos especifica que este valor debe ser 50, por lo que
y el enunciado nos especifica que este valor debe ser 50, por lo que 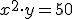 . Despejando
. Despejando
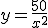 . Si sustituimos ahora esta expresión en la función que proporciona la superficie, se obtiene
. Si sustituimos ahora esta expresión en la función que proporciona la superficie, se obtiene 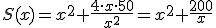 .
.
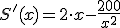 e igualando a 0 determinamos x,
e igualando a 0 determinamos x, 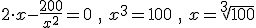 .
.
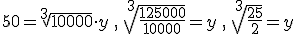 .
.
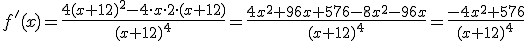 . Igualando a 0 para calcular el máximo, obtenemos la siguiente ecuación.
. Igualando a 0 para calcular el máximo, obtenemos la siguiente ecuación.
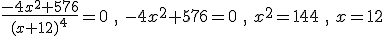 . Se desecha la solución negativa al no tener sentido en el contexto.
. Se desecha la solución negativa al no tener sentido en el contexto.
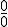 . Utilizaremos la regla de L'Hopital
. Utilizaremos la regla de L'Hopital
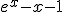 , entonces g'(x)=
, entonces g'(x)=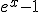 . Así
. Así