1.1. Funcionando al máximo
Existe la creencia equivocada en los estudiantes de matemáticas que una función tiene su máximo y su mínimo en aquellos puntos donde la derivada es nula ¿Esto es cierto siempre? ¿En algunas ocasiones no es cierto? Veámoslo con un sencillo ejemplo. Un automóvil circula por una autovía con el control de velocidad activado para mantener la velocidad constante (sin pasar de la velocidad permitida de 120km/h) durante 1 hora y media ¿Cuál será el máximo de la distancia recorrida?
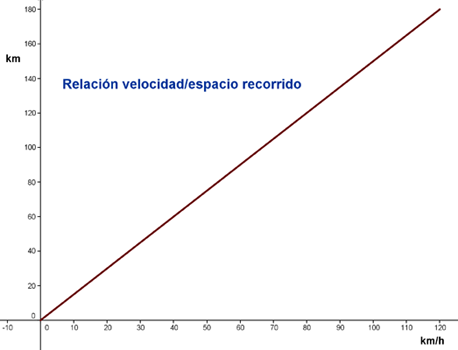 |
Veamos una pequeña tabla y una gráfica que relaciona la velocidad y la distancia recorrida en kilómetros.
| Velocidad en Km/h | Distancia en Km |
| 0 | 0 |
| 10 | 15 |
| 50 | 75 |
| 60 | 90 |
| 100 | 150 |
| 120 | 180 |
Así podemos indicar que la función que relaciona la distancia recorrida en función de la velocidad es f(x) = 1,5x
Puedes ver, tanto en la tabla como en la gráfica que la distancia recorrida máxima la alcanzará el automovil al circular a la velocidad máxima, es decir, al circular el coche a 120 km/h (el auto recorrerá 180 km). Sin embargo la derivada de la función f(x) es f '(x) = 1,5 y no se anulará nunca. Analogamente, podemos razonar para calcular el mínimo de la distancia recorrida, ya que podemos indicar sin duda alguna que el mínimo de la distancia recorrida se conseguirá al circular el coche a 0 Km/h, es decir, al encontrarse parado.
Con esto comprobamos que algunas veces, los valores máximo y mínimo de una función no necesariamente se alcanzan en lugares donde la derivada se anula.
Veamos las condiciones necesarias para calcular los valores máximos y mínimos de una función.
Para buscar los máximos y mínimos absolutos de una función, no nos interesa solo calcular aquellos puntos con derivada nula, ya que entre ellos nos encontraremos con extremos relativos de la función. En estos problemas nos interesan también los extremos del intervalo estudiado. Veamos algunas indicaciones
1. Si la función f(x) es derivable en [a,b], los máximos y mínimos absolutos se encontrarán en el conjunto formado por los puntos singulares (derivada nula) y los extremos del intervalo.
Para calcularlos debemos
- Resolver la ecuación f '(x)=0 .
- Seleccionar las raíces que se encuentran entre a y b (x1,x2,...)
- Calcular f(a),f(x1),f(x2),...,f(b).
- Entre estos valores calculados, determinaremos el máximo y el mínimo.
2. Si la función f(x) no es derivable en algún punto de [a,b], aunque sí continua, determinamos también el valor de f en dicho punto, ya que es posible que sea un máximo o un mínimo.
3. Si f no es continua en algún punto x0 de [a,b], estudiaremos la función en dicho punto.
 |
|
Fotografía tomada del |
En la localidad onubense de Higuera de la Sierra se celebra la segunda cabalgata de Reyes de Reyes Magos más antigua de España. Tras finalizar la cabalgata, se lanzan fuegos artificiales desde un lugar cercano. Entre éstos, se lanza una bengala verticalmente, hacia arriba , con una velocidad de 100 m/s.
¿Qué altura máxima alcanzará la bengala, si la ecuación de posición es h(t) = 100·t -10·t2?
 Teresa tiene en su casa un jardín de forma semicircular, y pretende construir en ese terreno una fuente de forma rectangular, de tal forma que el área de la fuente sea máxima, ya que quiere incluir en ella unos nenúfares decorativos. Si la función que indica el área del rectángulo inscrito es
Teresa tiene en su casa un jardín de forma semicircular, y pretende construir en ese terreno una fuente de forma rectangular, de tal forma que el área de la fuente sea máxima, ya que quiere incluir en ella unos nenúfares decorativos. Si la función que indica el área del rectángulo inscrito es 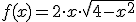 , indica cuál será el área máxima (x puede variar desde -2 hasta 2)
, indica cuál será el área máxima (x puede variar desde -2 hasta 2) |
| Foto de Alessandro Quisi tomada del Banco de Imágenes del ITE. |
EL consumo de gasolina de los coches deportivos suele ser muy alto, alrededor de 14 litros cada 100 kilómetos, lo que no suele ser lo más recomendable para cuidar el medioambiente.
A pesar del consumo y del coste para el medioambiente, Fran desea comprarse un deportivo, marca Ferrarini, pero teme el gasto que puede tener en gasolina al circular con el auto. Su cuñado, observa en un revista especializada que el Ferrarini Rampanto, circulando a una velocidad de x kilómetros hora tiene un consumo que viene expresado con la función 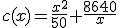 , con el coste en céntimos de euro. ¿Cuál será la velocidad a la que debe circular el coche para que el consumo sea más económico?
, con el coste en céntimos de euro. ¿Cuál será la velocidad a la que debe circular el coche para que el consumo sea más económico?
Una editorial pretende imprimir un libro con 500 cm2 de área. Los márgenes inferiores y laterales deben medir 1 cm. y 3 el superior. Determina las dimensiones de la página que permitan obtener el mayor área posible impresa (el área viene dada por la expresión 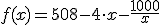 , donde x representa el ancho de la hoja).
, donde x representa el ancho de la hoja).
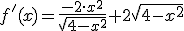 entonces
entonces 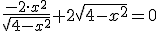 ,
, 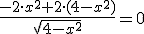 . Así obtenemos
. Así obtenemos
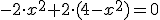 ,
, 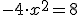 ,
, 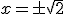 .
.
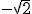 )= -4 (área negativa)
)= -4 (área negativa)
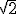 ) = 4
) = 4
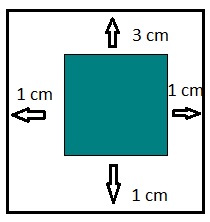 Calculemos en primer lugar la derivada de la función indicada para determinar los puntos críticos.
Calculemos en primer lugar la derivada de la función indicada para determinar los puntos críticos.
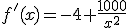 .
.
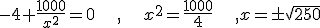
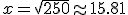 cm es la solución del problema.
cm es la solución del problema.