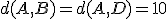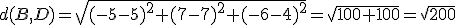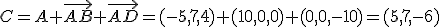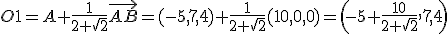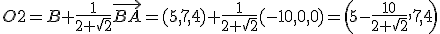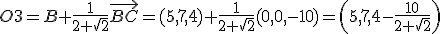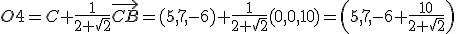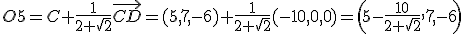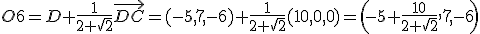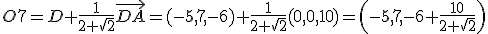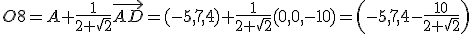2.2 Pintando con medidas
|
|
Observa el vídeo de la derecha. Aquí puedes apreciar algunos retoques fotográficos realizados con imaginación y utilizando vectores al identificar elementos comunes de los animales que se han relacionado. Para hacer una de estas combinaciones se va a partir de la estructura de un pulpo.
El pulpo tiene 8 patas como observamos en la fotografía.
 |
| Pulpo. Imagen obtenida del Instituto de Tecnologías de la Eeducación |
Para conseguir situar las ocho patas del pulpo se ha partido de un cuadrado sobre el que se ha situado otro cuadrado girado, consiguiendo los ocho puntos tal y como se observa en la imagen animada. El cuadrado primero tiene por vértices A, B, C y D. Los puntos de corte de los dos cuadrados determinan un octógono sobre el que se va a distribuir las patas del pulpo que después servirá para diseñar otra imagen como las observadas en el vídeo.
Observa en la imagen animada la forma en la que se obtienen los distintos vértices del octógono:
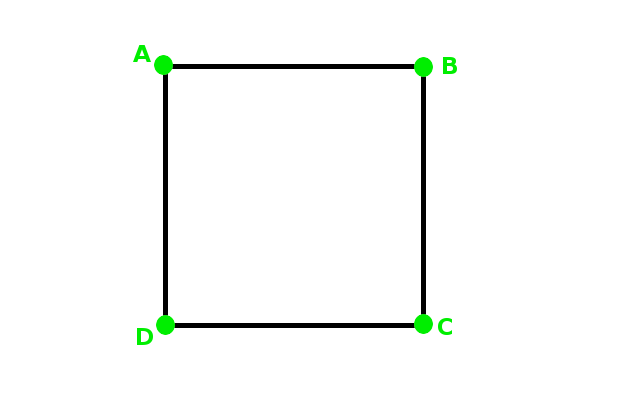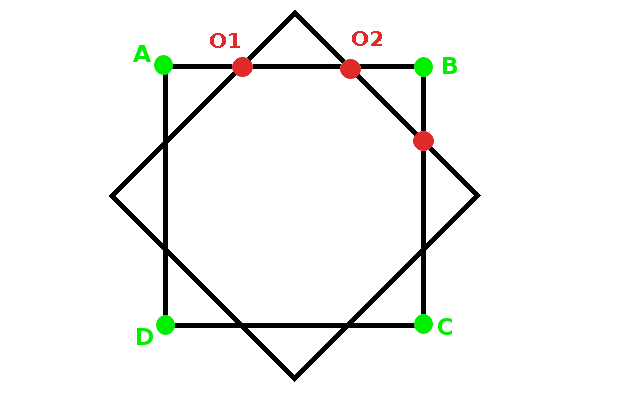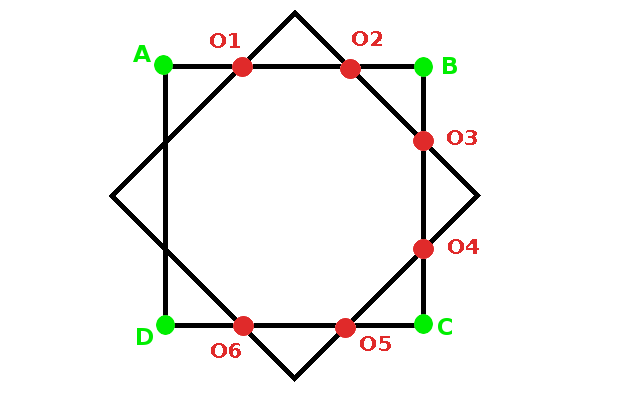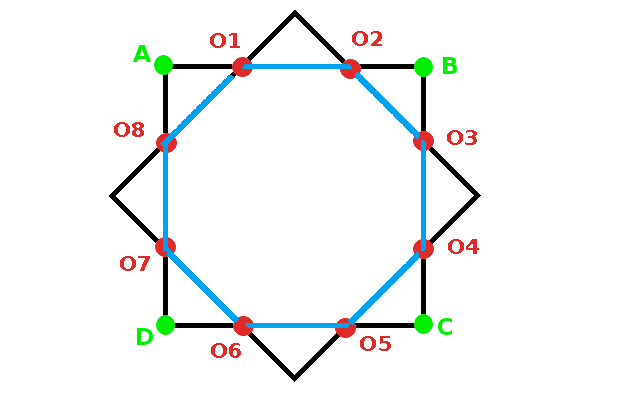 |
Como puedes observar es una imagen que guarda bastantes simetrías que podemos utilizar para la resolución del ejercicio que nos van a plantear. De este octógono nos proporcionan los vértices A=(-5,7,4), B=(5,7,4) y D=(-5,7,-6). Para resolver el ejercicio que planteamos de cara al futuro diseño debemos:
1.- ¿Son A, B y D vértices de un cuadrado?
2.- En caso de serlo, calcula el vértice C.
3.- Si la distancia que hay de A al vértice O1 es 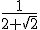 la distancia que hay de A a B, Calcula los vértices del octógono.
la distancia que hay de A a B, Calcula los vértices del octógono.
Observa el siguiente juego del cubo de Rubik y manéjalo ya que está relacionado con el ejercicio posterior. En este juego puedes realizar los movimientos del cubo. Cada astronauta de la parte inferior realiza una acción distinta sobre el juego (el último de la derecha es el que se encarga de la musiquita):
|
|
| Cubo de Rubik. Animación gráfica obtenida de Juegos 29. |
Instrucciones:
- Arrastre el ratón para rotar la figura.
- Puedes arrastrar cada uno de los puntos anaranjado.
- Shift + arrastre vertical = zoom
Los sólidos platónicos, también conocidos como cuerpos platónicos, cuerpos cósmicos, sólidos pitagóricos, sólidos perfectos, poliedros de Platón o, con más precisión, poliedros regulares convexos; son cuerpos geométricos caracterizados por ser poliedros convexos cuyas caras son polígonos regulares iguales y en cuyos vértices se unen el mismo número de caras.
Reciben estos nombres en honor del filósofo griego Platón (ca. 427 adC/428 adC – 347 adC), al que se atribuye haberlos estudiado en primera instancia.
Esta lista es exhaustiva, ya que es geométricamente imposible construir otro sólido diferente de los anteriores que cumpla todas las propiedades exigidas, es decir, convexidad y regularidad.
|
|
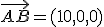
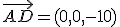
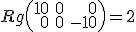 por tanto los tres puntos no están alineados.
por tanto los tres puntos no están alineados.
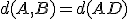
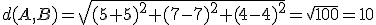
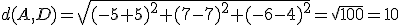
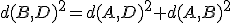 sabemos que
sabemos que