1.2 Posición relativa de puntos
 |
 |
Si tenemos dos puntos  y
y 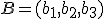 nos proponemos calcular el punto medio entre
nos proponemos calcular el punto medio entre 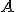 y
y  . Para ello vamos a hacer lo siguiente:
. Para ello vamos a hacer lo siguiente:
Calculamos el vector 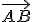 . Si al punto
. Si al punto 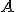 le sumamos el vector
le sumamos el vector 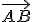 obtenemos el punto
obtenemos el punto 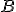 , por lo que para calcular el punto medio vamos a sumarle al punto
, por lo que para calcular el punto medio vamos a sumarle al punto 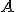 la mitad del vector
la mitad del vector 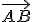 .
.
De esta forma: 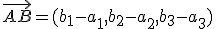
Por tanto, el punto medio será 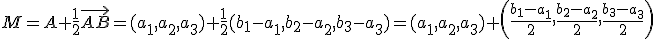
| PUNTO
MEDIO ENTRE DOS PUNTOS: En la escena de la derecha aparece un punto P=(p1,p2,p3) y otro punto Q=(q1,q2,q3). Aparece el vector que es el vector v=PQ y según lo que hemos visto anteriormente, representamos el punto M, punto medio entre P y Q. Te proponemos que en los siguientes apartados calcules el punto M, punto medio entre el punto P y el punto Q. 1.- P=(3,2,2) y Q=(1,4,6) 2.- P=(-1,4,-2) y Q=(1,4,6) 3.- P=(5,-3,-1) y Q=(3,5,5) 4.- P=(4,-1,7) y Q=(-2,5,3) |
Instrucciones:
|
1.- M=
2.- M=
3.- M=
4.- M=
| PUNTO
SIMÉTRICO: En la escena de la derecha aparece un punto P=(p1,p2,p3) y otro punto O=(o1,o2,o3). Aparece el vector v=PO y representamos el punto Q, que es el punto simétrico de P respecto a O. Gráficamente es muy fácil de obtener, basta con sumarle al punto P el doble del vector v Te proponemos que en los siguientes apartados calcules el punto simétrico de P respecto al punto O. 1.- P=(3,2,2) y O=(1,4,6) 2.- P=(-1,4,-2) y O=(1,4,6) 3.- P=(5,-3,-1) y O=(3,5,5) 4.- P=(4,-1,7) y O=(-2,5,3) |
Instrucciones:
|
1.- Q=
2.- Q=
3.- Q=
4.- Q=
| Entre las propiedades geométricas que podemos comprobar utilizando las propiedades de los vectores encontramos la de conocer si tres puntos del espacio están alineados o no. Para ello nos basamos en que dados tres puntos A, B y C, si estuvieran alineados, los vectores AB y AC serían linealmente dependientes | Instrucciones:
|
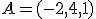 ,
, 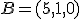 y
y 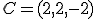 ?
?
Verdadero Falso
Verdadero Falso
Verdadero Falso
Verdadero Falso

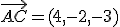
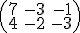 que es 2.
que es 2.
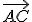 son linealmente independientes. Luego los tres puntos no están alineados.
son linealmente independientes. Luego los tres puntos no están alineados.