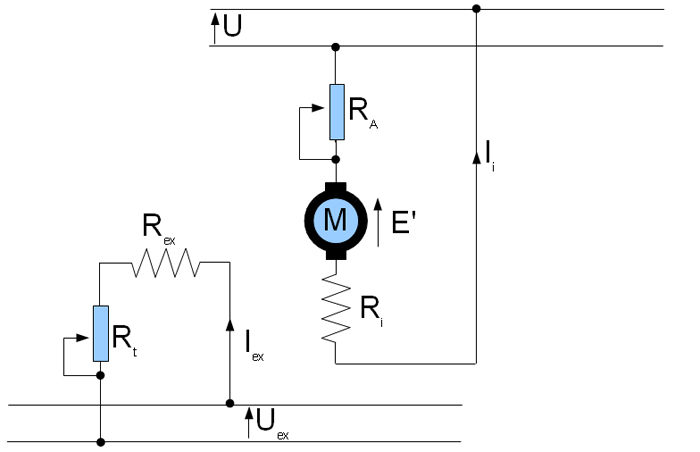
6.1. Motor excitación independiente
El esquema de un motor de excitación independiente es como el que se observa en la figura, distinguiéndose claramente dos circuitos eléctricos independientes, el de excitación o inductor, y el de inducido, por lo que podemos establecer, según la ley de Kirchhoff, dos ecuaciones eléctricas. RA es un reostato para regular Ii, e inicialmente su valor es cero.
|
|
| Imagen 19. Elaboración propia |
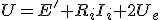
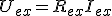
Donde 2Ue, es la caída de tensión que se produce en el contacto entre las delgas del colector y las escobillas, se cuantifica como una cantidad constante de 2 voltios, y si la tensión de alimentación del motor es razonablemente elevada se desprecia al hacer cálculos, ya que no se introduce un error muy significativo.
Las curvas características del motor suelen ser dos:
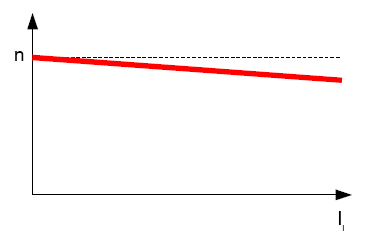
- la característica de velocidad en las que se representa como se
modifica la velocidad de giro en función de la intensidad de inducido mientras
se mantiene constate la intensidad de excitación.
En la excitación independiente la intensidad de excitación es simepre la misma y puesto que cien de otra alimentación, no cambia pase lo que pase en el inductor. Como el valor del flujo es proporcional a la intesidad de excitación independiente, se debe cumplir: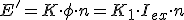
Como además en el inductor se cumple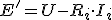
Igualando E', y despejando:
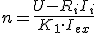
-
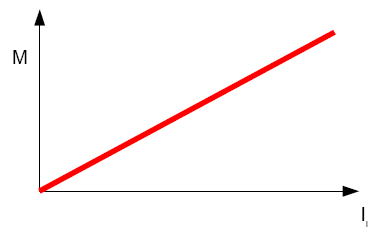
Y la característica de par, en la que se
representa la variación del par en función de la intensidad de inducido
mientras se mantiene constante la intensidad de excitación.
Por lo que se cumple:
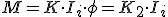
 |
 |
|
n=f(Ii) para Iex=cte Imagen 20. Elaboración propia |
M=f(Ii) para Iex=cte Imagen 21. Elaboración propia |
Calcular:
a) Tensión de alimentación.
b) Potencia absorbida, potencia útil y rendimiento.
c) Intensidad de cortocircuito.
d) Resistencia
del reóstato de arranque para limitar la intensidad en ese régimen a
e) Par motor y par de arranque suponiendo el flujo constante.