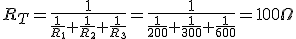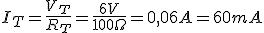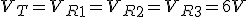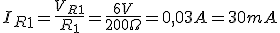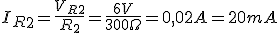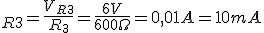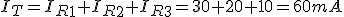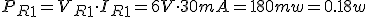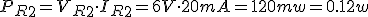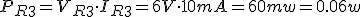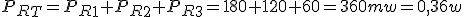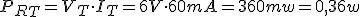11.1. Divisor de intensidad

Icono IDevice Actividad
  • Divisor de intensidad

Dos o más resistencias conectadas en paralelo forman un divisor de intensidad. De acuerdo con la primera ley de Kirchhoff o ley de los nudos, la corriente que entra en un nudo es igual a la suma de las corrientes que salen de él, por lo que seleccionando valores adecuados de resistencias se puede dividir una corriente en los valores que se precisen.

 

 


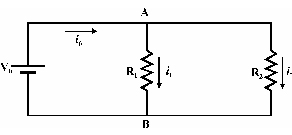
En el caso particular de un divisor de dos resistencias, es posible determinar las corrientes parciales que circulan por cada resistencia, I1 e I2, en función de la corriente total I, sin tener que calcular previamente la caída de tensión en la asociación. Para ello se utilizan las siguientes ecuaciones de fácil deducción:

La resistencia equivalente a la asociación de dos resistencias en paralelo resulta ser:

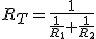
R_T=\displaystyle\frac{1}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}}

Es decir:

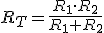
R_T=\displaystyle\frac{R_1\cdot{}R_2}{R_1+R_2}

Y como, según la ley de Ohm:

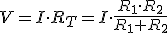
V=I\cdot{}R_T=I\cdot{}\displaystyle\frac{R_1\cdot{}R_2}{R_1+R_2}

Para calcular IR1, aplicando de nuevo la ley de Ohm, tenemos:

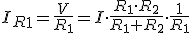
I_R_2=\displaystyle\frac{V}{R_2}= I\cdot{}\displaystyle\frac{R_1\cdot{}R_2}{R_1+R_2}\displaystyle\frac{1}{R_2}\cdot{}

Es decir:


Igualmente si repetimos los cálculos para IR2, obtenemos: 

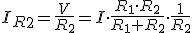
I_R_2=\displaystyle\frac{V}{R_2}= I\cdot{}\displaystyle\frac{R_1\cdot{}R_2}{R_1+R_2}\displaystyle\frac{1}{R_2}\cdot{}

Es decir:

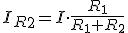
I_R_2=I\cdot{}\displaystyle\frac{R_1}{R_1+R_2}

Icono de iDevice Ejemplo o ejercicio resuelto
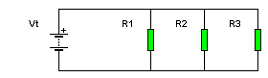A partir del esquema del circuito de la figura, y para los valores indicados
Vt=6V.
R1=200Ω.
R2=300Ω.
R3=600Ω.

Calcula:

  • La intensidad que atraviesa cada resistencia.
  • La caída de tensión en bornes de cada resistencia.
  • La potencia que disipa cada resistencia.
  • La potencia total que suministra la pila.

Icono de iDevice AV - Reflexión

Para que practiques nuevamente el ejercicio anterior, aquí tienes una tabla con distintos datos sobre el mismo circuito que se ha resuelto paso a paso: En el encabezamiento de cada columna tienes la fórmula, como recordatorio, que debes aplicar en cada caso

 

V

R1

R2

R3

IR1

IR2

IR3

IT

PR1

PR2

PR3

 

 

 

 

IR1=V/R1

IR2=V/R2

IR3=V/R3

IT=VT/RT

P1=I1·V

P2=I2·V

P3=I3·V

15V

180Ω

90Ω

60Ω

             

10V

300Ω

100Ω

150Ω
          


 

30V

1,2kΩ

2,4kΩ

0,8kΩ

             

60V

18kΩ

36kΩ

12kΩ

             

28V

21kΩ

14kΩ

42kΩ

   


       

 

« Anterior | Siguiente »