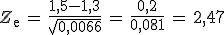2. Las redes sociales enganchan
Ejemplo o ejercicio resuelto
 |
¿Participas de forma activa en redes sociales?
Hoy en día, difícil es no estar en Tuenti, Facebook o Twitter. Imagino que esto no es nada nuevo para ti que harás un buen uso de las redes sociales para aprender y compartir información.
Sin embargo, aunque sea positivo el hecho de poder interactuar y compartir conocimiento con miles de personas, debes tener cuidado con el número de horas que pasas delante del ordenador, te lo digo por propia experiencia, y es que después vienen los dolores de cabeza y de espalda y hay que cuidarse.
Y como este tema no podía pasar desapercibido a la empresa farmacéutica de nuestra localidad, analizando el inventario, ha detectado como en el último año ha aumentado la venta de antiinflamatorios de forma considerable, sobre todo para dolores musculares y de espalda, en jóvenes de 12 a 18 años.
El motivo de este aumento, creen los responsables de la empresa, que es debido al aumento del uso del ordenador y de tener posturas no adecuadas delante de él, y esto se debe en gran parte al uso de internet y sobre todo a la participación activa en redes sociales.
Para comprobar estos datos, la empresa farmacéutica encarga a TisBet Survey que haga un estudio, tomando como muestra el alumnado del IES "Benito V.", para comprobar si hay diferencia entre el número de horas diarias que están sentados delante del ordenador el alumnado que tiene internet y no participa en redes sociales y el alumnado que sí participa de forma activa.
Para ello, se seleccionan a 100 alumnos que tienen internet en su casa y se les separa en dos grupos, aquellos que utilizan internet y participan de forma activa en redes sociales y los que utilizan internet pero no están en ninguna red social, formando cada grupo 70 y 30 alumnos, respectivamente.
Se les pregunta el número de horas diarias que pasan delante del ordenador, obteniendo para el primer grupo una media de 1,50 horas y desviación típica 0,5 horas, y par el segundo, 1,30 horas y desviación típica 0,3 h.
Si suponemos que la variable aleatoria número de horas sigue una distribución normal en los dos grupos, ¿es posible afirmar con un nivel de significación del 5% que hay diferencia de horas entre los alumnos que participan en redes sociales y los que no?
.
Actividad
Si X1 y X2 son variables aleatorias que siguen una distribución normal de
media desconocida y desviación típica conocida, X1~N(μ1,σ1) y X2~N(μ2,σ2), el
estadístico a utilizar para hacer un contraste de hipótesis para la diferencia de medias es:
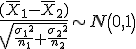
Siendo μ1 y μ2 los valores de las medias sobre los que se plantea la hipótesis nula, σ1 y σ2 las desviaciones típicas y n1 y n2 los tamaños de las muestras tomadas.
Además, para un contraste de hipótesis bilateral del tipo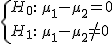 
la región crítica viene dada por: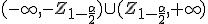 
AV - Pregunta de Elección Múltiple
|
|
Imagen de jlastras bajo licencia Creative Commons |
Una famosa cadena de tiendas de ropa y calzado quiere hacer un estudio de las ventas realizadas durante las rebajas de enero en los dos últimos años, para ver si han existido diferencias significativas entre ambos, teniendo en cuenta que el segundo año se crearon 12 tiendas nuevas.
Se considera que el dinero obtenido en las ventas en cada uno de los años sigue una distribución normal con desviación típica igual a 50 €.
En el primer año las 63 tiendas de la empresa, obtuvieron una venta media muestral de 1525,40 € y en el segundo año, las 75 tiendas obtuvieron una venta media muestral de 1642,50 €.
1) ¿Cuál será el contraste de hipótesis que hay que plantear para decidir si existen diferencias entre las ventas en rebajas en los dos años?
| |
|
| |
|
|
| |
|
|
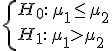
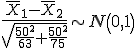
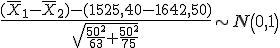
(-1,96;1,96)
| |
|
(-∞,-1,96)υ(1,96,+∞)
| |
|
(-∞,1,96)
|
|
Como Zexp= -13,7 y este valor no pertenece a la región crítica, aceptamos la hipótesis nula
| |
|
Como Zexp= -13,7 y este valor no pertenece a la región de
aceptación, rechazamos la hipótesis nula
| |
|
Como Zexp= -1,7 y éste pertenece a la región de
aceptación, aceptamos la hipótesis nula
|
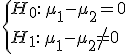
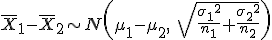
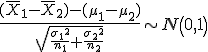
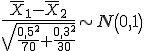
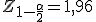Objetivos