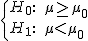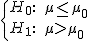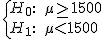1.1 ¡Échate a un lado!
Ejemplo o ejercicio resuelto
 |
| Imagen de hdaniel bajo licencia Creative Commons |
El otro día, mientras esperaba el autobús presencié una situación bastante curiosa. Resulta que había una máquina expendedora de refrescos y zumos y varios chicos comentaban entre ellos que los envases de refrescos parecían que cada vez tenían menos contenido. ¿Podría ser esto verdad? ¡Qué escándalo! ¿no? ¡La empresa de refrescos engaña al consumidor!
En el envase aparece que el contenido es de 25 cl ¿Será cierto o tendrán razón los chicos y es menor? Según afirma la empresa el contenido de cada envase tiene una media de 25 cl y una desviación típica de 0,8 cl. Analizadas 36 latas, se observa que la media de esa muestra es 24,88 cl. ¿Quién tiene razón con un nivel de significación del 6%?
Curiosidad
 |
|
| Imagen de jlmaral bajo licencia Creative Commons |
Fíjate que en el ejercicio resuelto, en ningún momento hemos dicho nada sobre la distribución de probabilidad de la variable aleatoria X. No decimos que la variable siga una distribución normal, pero es que no nos hace falta, pues como vimos en el tema 4 de la unidad anterior, si el tamaño de muestra es suficientemente grande, aplicando el Teorema Central del Límite, la media muestral sigue una distribución normal de media la media de la variable aleatoria y desviación típica, la de la variable dividida entre la raíz cuadrada del tamaño de la muestra.
Por tanto, siempre que planteemos un contraste de hipótesis sobre la media de una variable aleatoria, y el tamaño de muestra sea suficiente (≥30), el estadístico del contraste será:
Importante
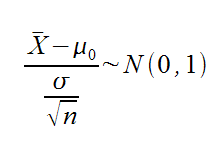
Si planteamos un contraste de hipótesis unilateral para la media de una variable aleatoria con un nivel de significación α, las regiones críticas del contraste vendrán dadas por:
| Contraste |
|
|
| Región Crítica |
|
|
AV - Reflexión
 |
| Imagen de KamalSelle bajo licencia Creative Commons |
Los ingenieros de un equipo de Fórmula 1 están probando un nuevo motor para sus monoplazas. Para que todo funcione correctamente una de las piezas deben durar de media al menos 1500 horas.
Puestos a comprobar si el motor se adapta a las necesidades del equipo, seleccionan una muestra aleatoria de 70 motores y en cada una de ellos analizan la duración de esa pieza concreta. Pues bien, en esa muestra llegan a la conclusión de que la duración media de la pieza es 1464 horas y además, de experiencias anteriores, se sabe que la desviación típica de la duración de las piezas es 180 horas. ¿Pueden considerarse buenas las piezas bajo un nivel de significación del 1%?
Para saber más
En este vídeo te mostramos otro ejemplo de contraste de hipótesis para la media de una variable aleatoria. Aquí cambia un poco la forma de expresar la región crítica y es que la da para ver la decisión simplemente a partir de la media muestral, pero en el fondo es lo mismo, pues lo único que hace es igualar el estadístico al extremo del intervalo y despejar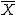 
. Puedes hacerlo como quieras.