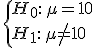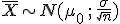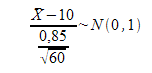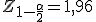1. Un medicamento tiene que ser efectivo
 |
| Imagen de xornalcerto bajo licencia Creative Commons |
Nuestra empresa farmacéutica va a lanzar al mercado un nuevo medicamento en forma de pastillas para combatir la alergia primaveral que tantos estragos causa cada vez a más población. Alergtin es el nombre de este medicamento y entre otros componentes, cada comprimido tiene que contener 10 mg de rupatadina que es el principio activo del antihistamínico.
La empresa cree que la máquina que fabrica estos comprimidos funciona correctamente, pero para asegurarse le piden a Tisbet Survey que les haga un control de calidad sobre esas pastillas, pues si no es así las consecuencias pueden ser fatales. Si tiene menos cantidad el medicamento puede ser inocuo y no hacer ningún efecto, mientras que si tiene más puede tener efectos secundarios en el paciente, así que es absolutamente necesario asegurarse que en cada comprimido hay 10 mg de rupatadina.
En Tisbet Survey llegan en primer lugar a la conclusión de que la cantidad de rupatadina en cada dosis sigue una distribución normal de media desconocida pero de desviación típica 0,85. Tras esto, toman una muestra de 60 pastillas y en ellas la cantidad media de rupatadina por comprimido es 9,36 mg. ¿Puede asegurarse con un nivel de significación del 5% que la máquina funciona correctamente y que por tanto el medicamento es correcto?
Si X es una variable aleatoria que sigue una distribución normal de media desconocida y desviación típica conocida, X~N(μ,σ), el estadístico a utilizar para hacer un contraste de hipótesis sobre la media es:
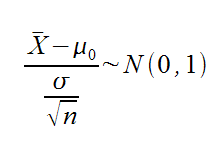
Siendo μ0 el valor de la media sobre el que se plantea la hipótesis nula, σ la desviación típica y n el tamaño de la muestra tomada.
Además, para un contraste de hipótesis bilateral del tipo 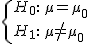 la región crítica viene dada por:
la región crítica viene dada por: 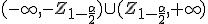
 |
| Imagen de Daquella manera bajo licencia Creative Commons |
El gasto medio semanal en gasóleo de los comerciales de una importante empresa de alimentación el año pasado siguió una distribución normal de media 43€ y una varianza de 16. Para ver si el gasto se mantiene, se ha cogido una muestra de 120 comerciales de la empresa y se ha analizado el gasto en una semana elegida al azar y parece que éste ha subido, pues de media, se han gastado 44,88 € semanales. ¿Puede afirmarse con un nivel de significación del 3% que el gasto en gasóleo se mantiene?
1) Para resolver este problema, el contraste de hipótesis que hay que plantear es:

| |
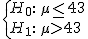
| |
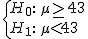
|
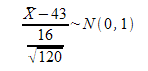
| |

| |
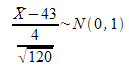
|
|
(1,88; +∞)
| |
|
(-∞; -1,88)
| |
|
(-∞; -2,17)U(2,17; +∞)
|
|
Se acepta porque Zexp=1,28 y no pertenece a la región crítica
| |
|
Se acepta porque Zexp=5,14 y no pertenece a la región crítica
| |
|
Se rechaza porque Zexp=2,41 y pertenece a la región crítica
| |
|
Se rechaza porque Zexp=5,14 y pertenece a la región crítica
|