3.3. Con la normal... a todas partes
 |
| Imagen de Andres Rueda bajo licencia Creative Commons |
Ahora ya sí que podemos calcular cualquier probabilidad normal.
Bueno, casi, y es que, la media de una distribución no tiene porqué ser siempre cero, ¿no? Por ejemplo, las ganancias mensuales de uno de los casinos que frecuentan Blanca y Gonzalo son aproximadamente de 18.500 € de media, la vida útil de las máquinas tragaperras del casino, como la que tienes a la izquierda es de 8,4 años, el número medio de clientes que acuden diariamente al bar La Tertulia, es de 254, y así podríamos poner un montón de ejemplos. Bueno, y tampoco la desviación típica va a ser siempre uno.¡Seguro que va tener distintos valores!
Entonces, ¿qué hacemos? ¿No habíamos dicho que con un folio íbamos a tener suficiente?
Pues así es querido alumno o querida alumna. Tan solo hemos de hacer una pequeña operación para llevarnos cualquier distribución Normal a una N(0 , 1) y ese proceso se llama TIPIFICAR. Cuando tengamos esto, ya si te prometemos que no nos hace falta nada más, que podremos calcular la probabilidad de que una televisión dure 20 años , que una bombilla se funda en un par de meses o de que tengamos que ir al médico porque nuestro nivel de colesterol no esté muy allá.
Importante
Tipificar una variable aleatoria continua que sigue una distribución normal de parámetros μ y σ, consiste en convertirla en una Normal de parámetros 0 y 1. Para ello, se le resta a la variable el valor de la media y se divide todo por el valor de la desviación típica. Es decir:
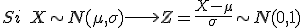
Por ejemplo, supón que X~N(14 ; 3,1) y necesitas calcular la probabilidad de que X sea menor que 11. Procederíamos así:
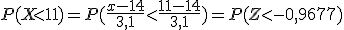
Y eso ya lo calcularíamos como en el apartado anterior, pues Z es ya una distribución N(0,1).
De todas formas, no te preocupes que con los siguientes ejemplos, seguro que lo vas a entender.
Ejemplo o ejercicio resuelto
En este primer ejemplo, vamos a aplicar la distribución normal a la fabricación de coches. Fíjate cómo resuelve la situación en el siguiente vídeo:
Segundo ejemplo. Hay que vigilar un poquito el peso...
 |
| Imagen de Bocadorada bajo licencia Creative Commons. |
Y tercer ejemplo, como la salud preocupa a todo el mundo, ahora hablamos de uno de los problemas que tiene buena parte de nuestra población en la sedentaria sociedad actual; el colesterol.
La distribución normal tiene muchísimas aplicaciones en la medicina pues muchos indicadores se distribuyen según un modelo normal. En este ejemplo, vemos que el nivel de colesterol en sangre de una persona se distribuye según una normal.
El enunciado nos dice que en una ciudad de 300.000 habitantes el nivel de colesterol en sangre sigue una distribución normal de media 192 y varianza 144. Nos pide calcular la probabilidad de que una persona elegida al azar tenga un nivel de colesterol comprendido entre 186 y 200, el número de personas con nivel de colesterol elevado, considerándose colesterol elevado si es superior a 235 y por último, nos pide determinar un nivel de colesterol de forma que el 84,2% de la población tenga un nivel superior a ese.
En la presentación que sigue está la solución de estas cuestiones.
Curiosidad
Fíjate que en este vídeo. Se aplica la distribución normal al tiempo de ejecución de una obra. ¡Si es que vale para todo!
Aquí, al final, la probabilidad la calculan de forma un poco distinta. Nosotros nos iríamos a la tabla directamente con el valor que nos sale al tipificar. Comprueba que es el mismo en la tabla.
AV - Pregunta de Elección Múltiple
 |
Hemos dicho al principio de este apartado que el número de clientes diarios del bar La Tertulia es de 254. Vamos a suponer que X=n.º de clientes diarios, sigue una distribución Normal y además, que la desviación típica es 5,4.
Lo mismo te has dado cuenta de que el número de clientes es una variable discreta, no puede haber 4 clientes y medio. Si es así, enhorabuena, esto marcha muy bien. Lo que ocurre es que a pesar de ser discreto, cuando los valores son muy grandes puede aproximarse a un modelo normal. en la próxima unidad veremos por qué es así.
Bueno, independientemente de esto, calcula las siguientes probabilidades:
1) P(X ≤ 260)
|
0,8438
| |
|
0,8686
| |
|
0,8461
| |
|
0,8665
|
|
Sí, puede estar tranquilo porque P(X >280) = 0
| |
|
Al contrario, es seguro que cualquier día le van a entrar más de 280 personas, pues la P(X>280) = 1.
| |
|
P(X>280) = 0,8599, así que no debe estar nada de tranquilo.
| |
|
Así así, pues la probabilidad de que un día acudan más de 280 personas es del 14,01%.
|
Para saber más
Para terminar, en este vídeo te muestran algunas propiedades de la distribución y las relaciones que indican los valores de la media y la desviación típica: