2. El previo. Un poco de paciencia

Importante

Imagen de thombo2 bajo licencia Creative Commons

Una variable aleatoria es continua si al realizar el experimento aleatorio, entre cada dos valores, el número de valores que puede tomar es infinito.

Por ejemplo, la altura de una persona, la longitud del dedo índice, el peso de un perro o el caudal de un río son variables aleatorias continuas, pues entre dos posibles valores puede tomar cualquiera que exista. Todo depende de la precisión de nuestro aparato de medida.

Ejemplo o ejercicio resuelto

Personas remando en el parque del Retiro de Madrid

Imagen de jl.cernadas bajo licencia Creative Commons

A la entrada de un parque, hemos realizado una encuesta sobre salud, y entre cosas, a la persona encuestada se le pregunta por su peso. Algunas no han querido responder, pero las que sí, nos han dado estos resultados:

60	75,3	81	86,6	68,1	70,4	69,4	88	94,1	72
77,4	82	57	70,5	65,2	65	81	82,2	63	70
80,5	59	60,5	65	71	73,6	88,4	90	92,5	101
87	76	65	69	72	74	98	88,3	60	76,6

¿Con qué probabilidad al elegir una persona pesará 84 kg? ¿Y 71,5? ¿Y 74 kg?

Importante

Si X es una variable aleatoria continua, la probabilidad de que tome un valor concreto es cero.

P[X = a] = 0, para cualquier valor de a.

Por tanto, en variables continuas, las probabilidades se calculan sobre intervalos y serán de esta forma:

P( a ≤ X ≤ b)
P( X ≥ a)
P( X ≤ b)

Además, como el signo "=" en un punto da probabilidad cero, en los intervalos anteriores da igual poner desigualdades estrictas o inclusivas, es decir, da lo mismo escribir ≤ ó < y es lo mismo escribir ≥ ó >.

Por ejemplo, si X es una variable aleatoria continua, P(X ≤ 2) = P(X < 2), pues la diferencia entre ambas es que entre el 2 o no, y como ya sabemos que la probabilidad del valor concreto 2 es cero, da igual que lo incluyamos o no.

Ejemplo o ejercicio resuelto

Como puedes pensar, es cierto que no se repite muchos valores en la tabla, pero no es menos cierto que la diferencia entre algunos de ellos es mínima. Está claro que no es lo mismo pesar 70 kilos que 98, pero, ¿hay mucha diferencia entre 70 kilos ó 70,4 kg?

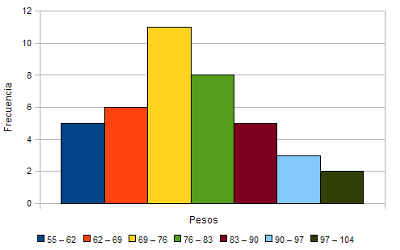
Es por esto por lo que en estas variables los datos se agrupan en intervalos. Vamos a hacerlo con los datos de nuestra tabla. Por ejemplo, lo hacemos así: Histograma de pesos asociado a la tabla

Intervalo	n.º de casos
55 - 62	5
62 - 69	6
69 - 76	11
76 - 83	8
83 - 90	5
90 - 97	3
97 - 104	2

Ahora sí tiene un poco más de sentido, calcular probabilidades.

Histograma de frecuencias relativas de la tabla Por ejemplo, según esta muestra, la probabilidad de que al elegir una persona al azar, ésta pese entre 69 y 76 kilos es 11/40:

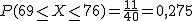
O la probabilidad de que al elegir una persona, ésta pese más de 76 kg es:

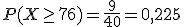
¿Entiendes ahora por qué en las variables continuas las probabilidades siempre se calculan sobre intervalos?

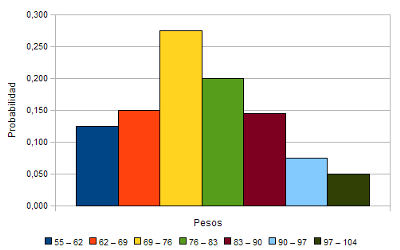
El gráfico de la izquierda nos muestra la distribución de probabilidad de los intervalos, pero, aún no es suficiente, porque ahora mismo podemos calcular sólo la probabilidad de que X esté en alguno de esos intervalos, si queremos la probabilidad de que una persona pese entre 70 y 80 kilos no podemos calcularla. De momento, claro.

Y es que, ahora sí que llegamos ya al equivalente de la función de probabilidad de las variables discretas. ¿Recuerdas el polígono de 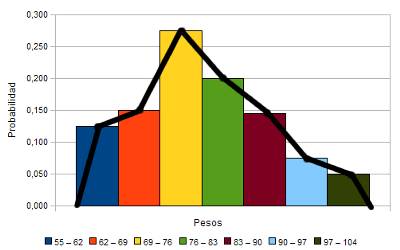Función de densidad marcada sobre el histograma asociado a la tabla frecuencias de los temas de estadística del curso pasado? Si no, no pasa nada.

Fíjate en el gráfico de la izquierda. Hemos unido los puntos medios de los intervalos mediante rectas (esto era el polígono de frecuencias.) Pues bien, si hacemos que los intervalos tengan una amplitud muy pequeña, esa línea poligonal va cogiendo cada vez una forma más redondeada, el de función, y se va a llamar función de densidad.

Esta función es la que marca las probabilidades en las variables aleatorias continuas, y es que cualquier probabilidad de un intervalo se calcula como el área encerrada bajo la función de densidad en ese intervalo.

Así, para una variable aleatoria continua, será necesario conocer su función de densidad para calcular cualquier probabilidad.

Ojo, la función de densidad siempre tiene que ser positiva y el área total encerrada por ella será 1, pues como siempre, la probabilidad de todo el espacio muestral es 1.