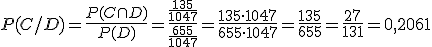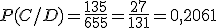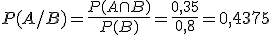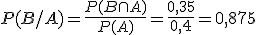2. ¿Y si ya ha ocurrido?
 |
| Imagen de Bananaguay con licencia Creative Commons |
Blanca ha introducido 10 bolas en una bolsa, 7 azules y 3 verdes. Saca una bola de la bolsa y es azul, a continuación, con la bola azul en la mano, le pregunta a Gonzalo, ¿cuál es la probabilidad de que la siguiente bola sea verde?
Gonzalo piensa que antes de sacar la primera bola, la probabilidad de sacar bola azul (A) y de sacar bola verde (V) son: P(A)=7/10 y P(V)=3/10.
Después de la primera extracción, como Blanca no ha devuelto la bola azul a la bolsa, quedan 6 azules y 3 verdes, un total de nueve bolas. Por lo tanto la probabilidad que le está pidiendo Blanca será:
P(2ª bola sea verde si la 1ª bola fue azul)=3/9=1/3.
En este caso la segunda extracción está condicionada por el resultado de la primera. En matemáticas cuando ocurre esto se representa P(V/A), es decir, cual es la probabilidad de que salga bola verde si ya ha salido una azul. Veamos en la siguiente escena este ejemplo de probabilidad condicionada. Mueve los deslizadores 1ª Extracción, 2ª Extracción y Probabilidad para ver el resultado.
Importante
Un suceso A está condicionado por otro B y se expresa A/B cuando el hecho de haber ocurrido B influye en la probabilidad de que ocurra A.
Se llama probabilidad condicionada del suceso A respecto del B y se denota P(A/B) al siguiente cociente:
Ejemplo o ejercicio resuelto
 |
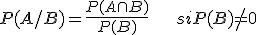
| Imagen de PePe García con licencia CC |
Recuerdas el ejercicio de los niños deportistas de Albarracín. Veamos cual es la probabilidad de que un niño vaya al campamento si hemos escogido a uno que hace deporte.
| Deporte | No Deporte |
Total |
|
| Campamento |
135 | 50 | 185 |
| No Campamento |
520 | 342 | 862 |
| Total | 655 | 392 |
1047 |
AV - Reflexión
En un experimento se sabe que P(A)=0,4, P(B)=0,8 y P(A ∪ B)=0,85. Calcula las siguientes probabilidades:
a) P(A ∩ B)
b) P(A/B)
c) P(B/A)
