1. Las ramas del árbol
 |
| Imagen de alvy con licencia Creative Commons |
Gonzalo y Blanca están pensando ampliar las apuestas habituales de su peña "Los Improbables" comprando también un décimo de la lotería nacional todas las semanas. Deciden ir a ver a su amiga María José para conocer mejor este juego, ella se lo podrá explicar desde un punto de vista matemático.
María José les aclara que en la Lotería nacional los jugadores apuestan por un número de 5 cifras, es decir, el espacio muestral son todos los números comprendidos entre 00.000 y 99.999. Durante el sorteo se extraen 5 bolas de 5 bombos diferentes, cada bola se corresponde con una cifra desde las decenas de millar a las unidades. Este juego por tanto está formado por más de un experimento aleatorio simple ya que es necesario realizar cinco extracciones de una bola de cada uno de los bombos, de manera consecutiva, para poder completar el juego. Es pues un claro ejemplo de lo que en teoría de probabilidades se conoce como experimento aleatorio compuesto.
Experimentos como el lanzamiento de un dado, el lanzamiento de una moneda, extraer una carta de una baraja e incluso extraer una bola de un bombo son experimentos simples, mientras que aquellos en los que fácilmente podemos distinguir dos o más etapas son experimentos compuestos; sería el caso del lanzamiento de dos dados, la extracción de varias cartas de una baraja o el lanzamiento de varias monedas.
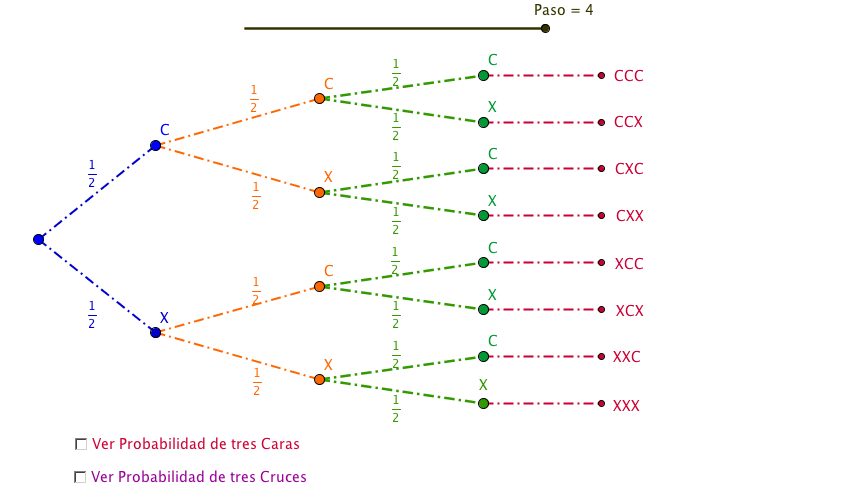
Para calcular la probabilidad de un suceso de un experimento compuesto se pueden usar varios métodos. Una de estos métodos consiste en usar los diagramas en árbol. En el diagrama, en cada paso, vamos escribiendo las probabilidades de los experimentos simples que componen nuestro experimento compuesto.
Se observa el camino de las ramas que nos conducen a la solución. El producto de las probabilidades de las ramas de dicho camino será la probabilidad del suceso solución.
En la siguiente escena estudiamos la probabilidad de que salga el número 61.731 en el próximo sorteo de lotería. La probabilidad de cada bola en cada bombo es de 1/10. Así pues la probabilidad de que salga el número 6 en el bombo de las decenas de millar es de 1/10. La probabilidad de que salga el número 1 en el siguiente bombo es de 1/10. Y así seguiríamos hasta el final.
En este caso la probabilidad buscada es:
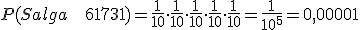
 |
| Imagen de MrB-MMX con licencia Creative Commons |
Blanca y Gonzalo están pasando la tarde en el local que tiene su peña de "Los Improbables". Se plantean un juego, lanzar una moneda 3 veces consecutivas. Se preguntan, ¿tiene la misma probabilidad sacar tres caras consecutivas de la moneda que sacar tres cruces?. Ayuda a nuestros amigos a responder la pregunta.
En la siguiente imagen tienes el diagrama de árbol del experimento: En urna donde hay dos bolas rojas y tres bolas verdes. Sacamos una bola, anotamos su color y la devolvemos a la urna. Realizamos este proceso tres veces.
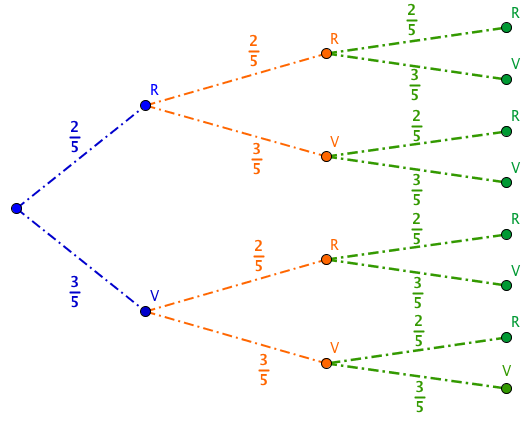 |
1. ¿Cuál es la probabilidad de que las tres bolas sean iguales?
|
(a) 35/125
| |
|
(b) 8/125
| |
|
(c) 27/125
| |
|
(d) 90/125
|
|
(a) 42/125
| |
|
(b) 38/125
| |
|
(c) 50/125
| |
|
(d) 32/125
|
|
(a) 18/125
| |
|
(b) 45/125
| |
|
(c) 27/125
| |
|
(d) 80/125
|