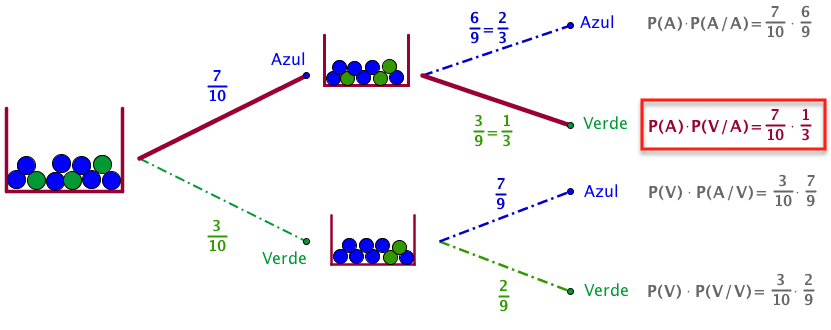
Recuerdas el juego de Blanca y Gonzalo con la bolsa y las 10 bolas, 7 azules y 3 verdes. Gonzalo, después de resolver el juego que le había propuesto Blanca, pregunta: ¿qué es más probable, que saque dos bolas verdes en una sola extracción o que saque una bola verde, la vuelva a introducir en la bolsa y vuelva a sacar otra bola verde?

María José que estaba atenta a la conversación, les pregunta si puede intervenir en el juego. Blanca asiente con la cabeza. El juego que propone Gonzalo, les dice María José, me va a servir para explicaros lo que es un suceso dependiente e independiente.

En el juego que proponía Blanca al principio, al realizar la segunda extracción, ésta estaba condicionada a una extracción anterior en la que ya había sacado una de las bolas de un determinado color, en este caso el color azul. Como no había devuelto la bola dentro de la bolsa, la segunda extracción dependía de la primera.

En el juego que propone Gonzalo tenemos dos partes. En la primera parte sacar dos bolas en una sola extracción equivale a realizar dos extracciones sucesivas sin reemplazamiento, es decir, sacamos una bola y, sin devolver ésta a la bolsa realizamos una segunda extracción. En este caso la segunda extracción dependerá de lo que haya salido en la primera. Es decir, serán dos sucesos dependientes.

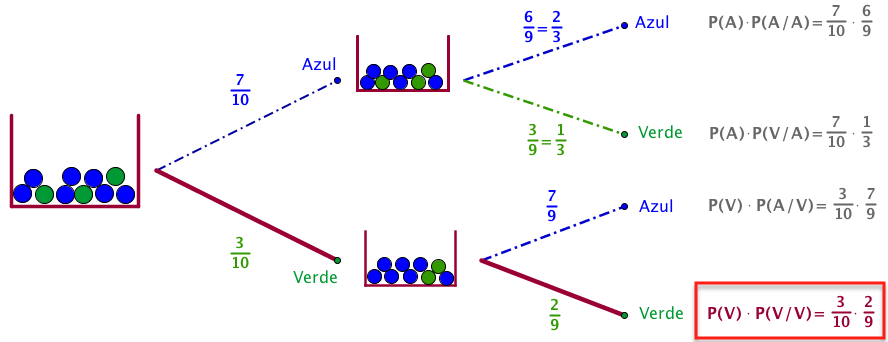Para calcular la probabilidad de sacar dos bolas verdes: P(Sacar dos bolas verdes)= P(Sacar la 1ª bola verde) · P(Sacar la 2ª bola verde / 1ª bola es verde), es decir 

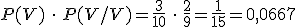
En la segunda parte nos pide que saquemos una bola, apuntemos su color y la devolvamos a la bolsa. A continuación, sacamos una segunda bola y anotamos su color. En este caso lo que ocurra en la segunda extracción no depende de lo que haya ocurrido en la primera, ya que hemos devuelto la bola a la bolsa y en el momento de realizar la segunda extracción estamos en las mismas condiciones que estábamos al realizar la primera. En este caso los sucesos son independientes ya que lo que ocurra en la primera extracción no influye en lo que pasará al realizar la segunda extracción.

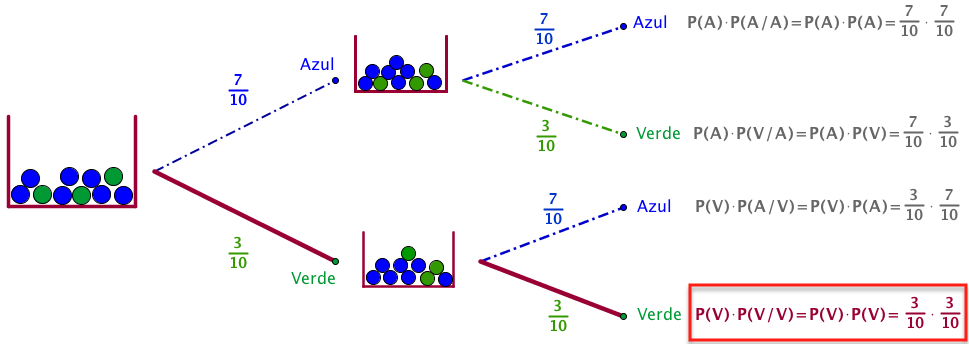Ahora la probabilidad de sacar dos bolas consecutivas verdes es P(Sacar dos bolas verdes)=P(sacar la primera bola verde)·P(sacar la segunda bola verde/1ª bola es verde), es decir:

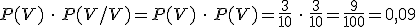
Podemos ver que cuando hay reemplazamiento es más probable sacar dos bolas verdes de forma consecutiva.

En estos dos vídeos puedes ver un ejemplo de probabilidad de sucesos dependientes y otro de probabilidad de sucesos independientes.

Probabilidad de sucesos dependientes	Probabilidad de sucesos independientes