4. A priori y a posteriori
|
|
| Así se hacen los tornillos y las tuercas |
Recuerdas la fábrica MITORNILLO, SA. En su estudio sobre la producción de tuercas quieren saber si una vez escogida una pieza defectuosa, cuál es la probabilidad de que provenga de la máquina A.
Veamos como realizar el estudio, los datos conocidos eran:
- Máquina A: 25% de producción y 2% de tuercas defectuosas.
- Máquina B: 45% de producción y 3% de tuercas defectuosas.
- Máquina C: 30% de producción y 1% de tuercas defectuosas.
Nos están pidiendo P(A/D)= Probabilidad de que la tuerca provenga de la máquina A dado que la es defectuosa. En este caso nosotros conocemos las probabilidades condicionadas contrarias. P(D/A)=0,02; P(D/B)=0,03; P(D/C)=0,01.
Para el cálculo de P(A/D) vamos a utilizar la definición de la Probabilidad Condicionada y el Teorema de la Probabilidad Total. Mueve el deslizador para ver como hacerlo:
Por lo que el cálculo de nuestra probabilidad,aplicando lo anterior, quedará como:

Dado un experimento aleatorio E y un conjunto de sucesos A1, A2, ..., An asociados a E tal que la probabilidad de cada uno de ellos es distinta de cero, son incompatibles dos a dos y tales que A1 ∪ A2 ∪ ... ∪ An = E, para cualquier otro suceso B de E con P(B)>0 se cumple que:
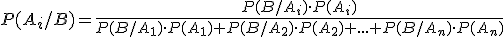
Este resultado se conoce con el nombre de Teorema de Bayes
La probabilidad P(Ai /B) recibe el nombre de probabilidad a posteriori. En nuestro ejemplo será la probabilidad de que una pieza provenga de la máquina A si sabemos que es defectuosa. Es la propiedad después de haber realizado un experimento, escoger una pieza defectuosa.
La probabilidad P(Ai ) recibe el nombre de probabilidad a priori. Son las probabilidades que conocemos antes de realizar el experimento. En nuestro caso la probabilidad de que una pieza provenga de la máquina A, B o C.
 |
| Imagen de velkr0 con licencia Creative Commons |
En una clase el 55% son chicos y el 45% son chicas. En el último examen de Matemáticas, han aprobado el 80% de los chicos y el 90% de las chicas.
(1) Calcula la probabilidad de que al elegir un estudiante al azar, haya aprobado.
(2) Sabiendo que un estudiante ha aprobado, calcula la probabilidad de que sea chica.
 |
| Thomas Bayes en Wikimedia Commons |
En las siguientes páginas puedes encontrar ejercicios con soluciones para practicar.
Página de J. Joaquín Seda en Thales.
Página vadenúmeros.es
Otra página en Slideshare de Luis Felipe Hernández
Aún más problemas en Gacetilla Matemática
Por último otro vídeo de juanmemol en YouTube, por si no nos ha quedado muy claro.