4. Las torres de Hanoi
 |
| Imagen de laurent KB bajo licencia Creative Commons |
¿Cuántos movimientos son necesarios para mover n discos?
Te damos una pista. El número de movimientos es una función exponencial.
En esta presentación puedes ver la solución a la cuestión que te planteábamos al principio.
Llamamos función exponencial a la que tiene por expresión analítica y=ax, siendo a un número real positivo distinto de 1.
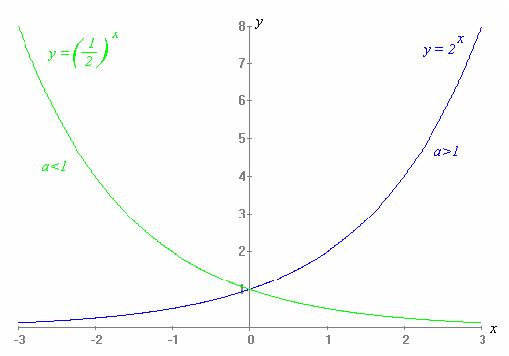 Son funciones continuas cuyo dominio es el
conjunto de los números reales. Son funciones positivas que pasan por los puntos
(0,1) y (1,a).
Son funciones continuas cuyo dominio es el
conjunto de los números reales. Son funciones positivas que pasan por los puntos
(0,1) y (1,a).
Si a>1, son funciones crecientes en todo su dominio.
Para valores de x muy grandes pero negativos, f(x) toma valores próximos a cero.
Para valores de x muy grandes, f(x) toma valores también muy grandes.
Cuanto mayor sea el valor de a, más rápido crecen estas funciones.
Si 0<a<1, son funciones decrecientes en todo su dominio.
Para valores de x muy grandes pero negativos, f(x) toma valores muy grandes.
Para valores de x muy grandes, f(x) toma valores próximos a cero.
Cuanto menor sea el valor de a, más rápido decrecen estas funciones.En la siguiente animación del Banco de imágenes y sonidos del ITE, puedes practicar representando gráficas de funciones exponenciales.
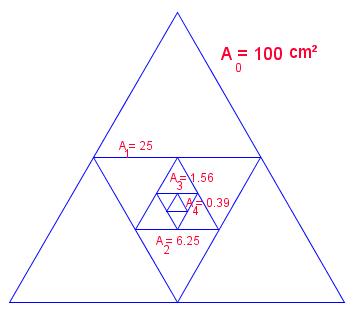
En un triángulo equilátero de área A0=100 cm2 se van inscribiendo nuevos triángulos como indica la figura:
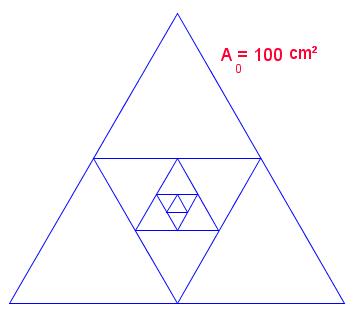
¿A partir de qué triángulo inscrito tendrá un área inferior a 10 cm2?
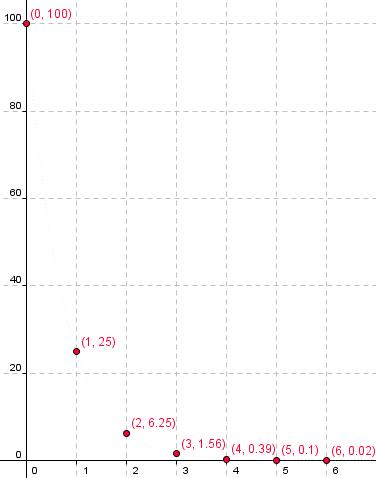
Representa en una gráfica la relación n.º del triángulo con su área en cm2.
¿A qué tipo de función corresponde la gráfica?
¿Cuál es su expresión analítica?

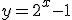 , sería:
, sería:
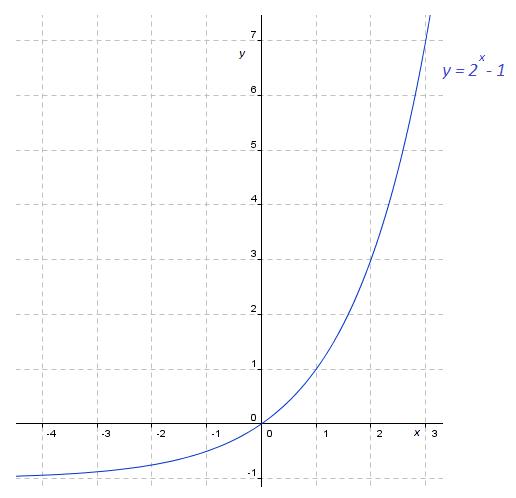
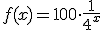 .
.