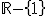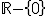2.1. Nos dividen y tenemos que ser racionales
 |
| Imagen de koluso bajo licencia Creative Commons |
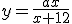 .
.
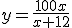 para valores de la x desde 1 a 12.
para valores de la x desde 1 a 12.
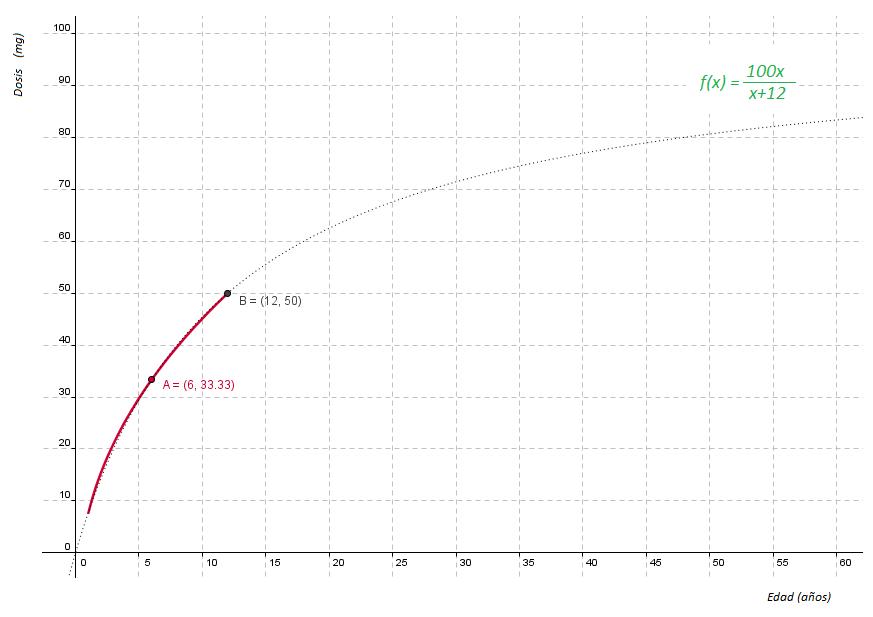
Una función racional está formada por un cociente de funciones polinómicas de la forma 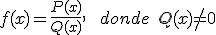 .
.
La función racional más sencilla es 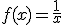 que corresponde a una función de proporcionalidad inversa cuya gráfica es una hipérbola.
que corresponde a una función de proporcionalidad inversa cuya gráfica es una hipérbola.
El dominio de una función racional está formado por el conjunto de los números reales menos aquellos valores de la x que anulan el denominador.

|
| Imagen de four_new_colours bajo licencia Creative Commons |
Adriana quiere cercar con una cuerda y forma rectangular un rincón de la caseta para guardar las muñecas de Inmaculada.
Si quiere que el área del recinto sea de 2 m2 y el trozo de cuerda no es muy grande, ¿cómo puede expresar el perímetro del cercado en función de una de las medidas del recinto?
¿A qué tipo de función corresponde la expresión encontrada?
¿Para qué valores tiene sentido dicha función?
Construye una tabla de valores para el perímetro y realiza un esbozo de la gráfica de la función.
¿Qué ocurre en la gráfica de la función cuando x toma valores próximos a cero?
¿Qué ocurre cuando la x va tomando valores cada vez más grandes (se acerca al infinito, a +∞)? ¿Y cuando toma valores negativos muy grandes (se acerca al infinito, a -∞)?
Calcula el dominio de las siguientes funciones racionales:
a) 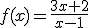 ; b)
; b) 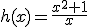 ; c)
; c) 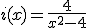 .
.
¿Qué función corresponde a la gráfica siguiente? ¿Cuáles son sus asíntotas? Razona la respuesta.
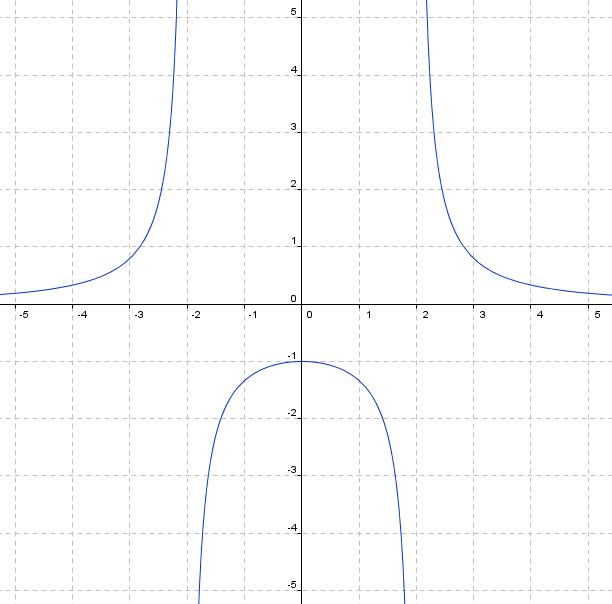
En la siguiente escena de Descartes creada por Mª José García Álamo puedes ver el comportamiento de estas tres funciones racionales:
- f(x)=1/(x + 5),
- g(x)= 3x /(x2 -25)
- h(x)=(x - 2) /(x2 + 1).
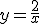 .
.
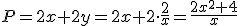 .
.
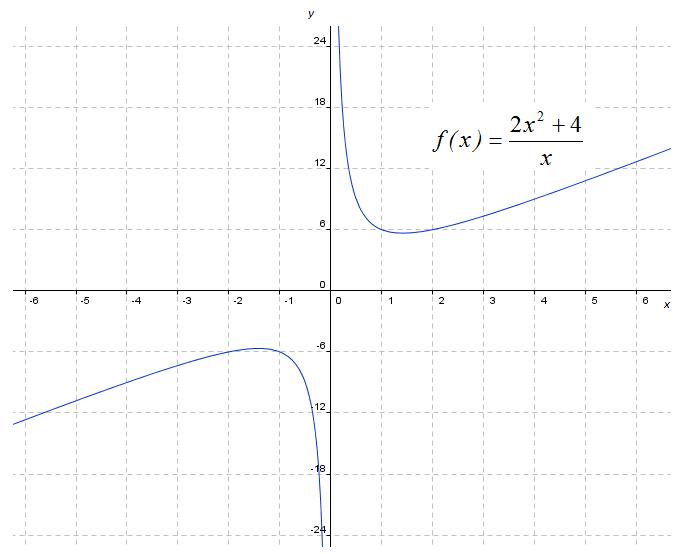
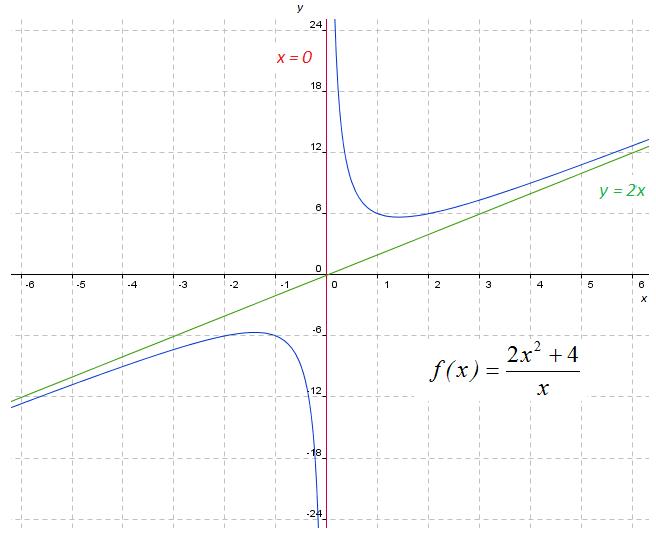
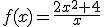 corresponde a una suma
de dos funciones, una función lineal g(x)=2x y una función de proporcionalidad inversa
corresponde a una suma
de dos funciones, una función lineal g(x)=2x y una función de proporcionalidad inversa 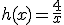 , formando un cociente de funciones polinómicas. A este
tipo de función se le llama función
racional.
, formando un cociente de funciones polinómicas. A este
tipo de función se le llama función
racional.