4.1. La montaña rusa
Ignacio, el padre de Inmaculada se marchó con los nietos del gerente de TRANS VELOX a la montaña rusa. Mientras tanto, nos quedamos hablando con Adriana, la madre de Inma, que nos comentaba que las subidas y bajadas que había en la montaña rusa eran muy grandes, pero que este año aún eran mayores las subidas de precios en las bebidas y raciones de comida que servían en la caseta, a pesar de que cada vez el nivel adquisitivo era menor ya que cada vez había más personas desempleadas.
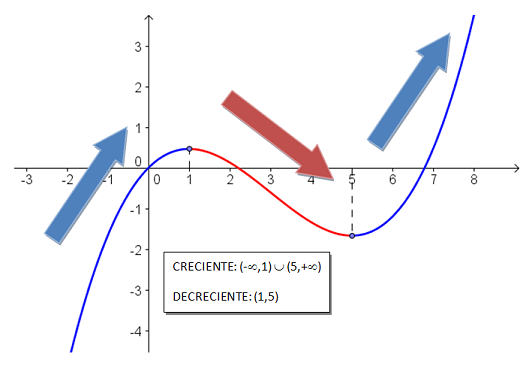
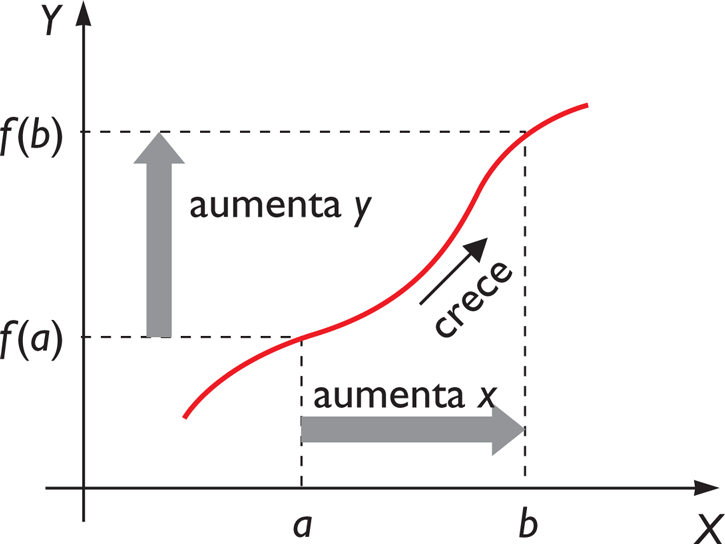
Como recordarás las funciones también presentan subidas y bajadas. El crecimiento y el decrecimiento de una función es algo que ya hemos estudiado antes. Básicamente una función es creciente si, al aumentar la variable independiente, x, también aumenta el valor de la función, f(x). Es decreciente, si al aumentar el valor de x, disminuye el de f(x). No olvides que las gráficas se "leen" de izquierda a derecha.
Actividad
Una función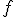 
es estrictamente creciente en un intervalo (a,b) si y sólo si:
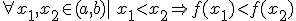
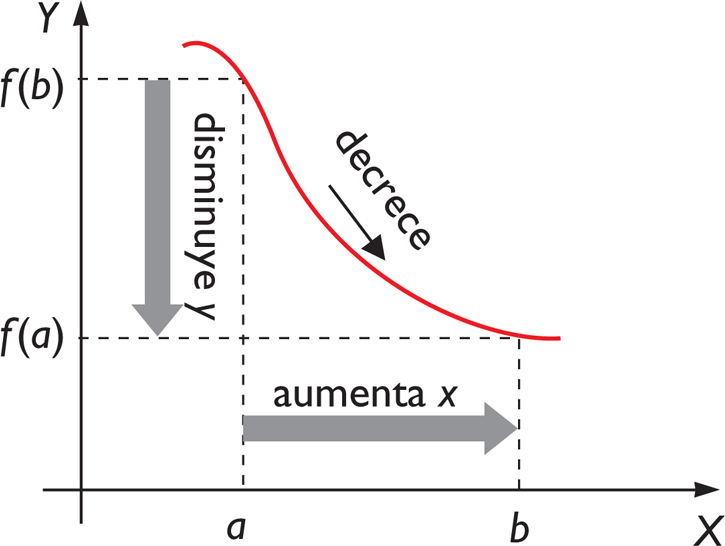
Una función 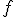es estrictamente decreciente en un intervalo (a,b) si y sólo si:
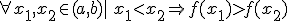
Uno de los nietos del gerente de TRANS VELOX se empeñó en montarse en la caída libre y yo no sé, si alguna vez habéis estado en una atracción de feria donde se alcanza el punto máximo de altura, pero la verdad es que impresiona.
En este apartado veremos como las funciones se comportan de forma parecida a las atracciones y cuando subimos hasta un punto determinado y comenzamos a bajar, decimos en matemáticas que estamos en un máximo, que puede ser relativo, si durante el trayecto nos encontramos otros puntos máximos mayores, o absoluto si es el mayor de todos.
Lo mismo ocurre cuando bajamos y comenzamos a subir, entonces hablamos de mínimos relativos y mínimos absolutos.
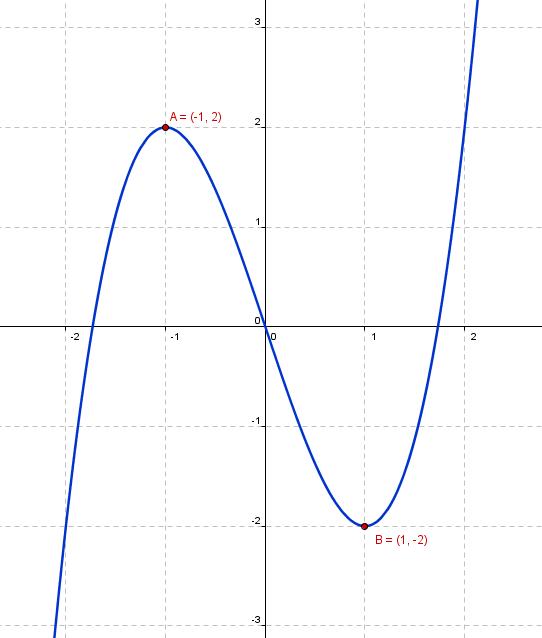
En la gráfica anterior veíamos claramente como la función tenía un máximo relativo en (-1,2) y un mínimo relativo en (1,-2).
Y como te habrás dado cuenta, los llamamos relativos ya que existen valores mayores y menores que ellos en la gráfica.
Actividad
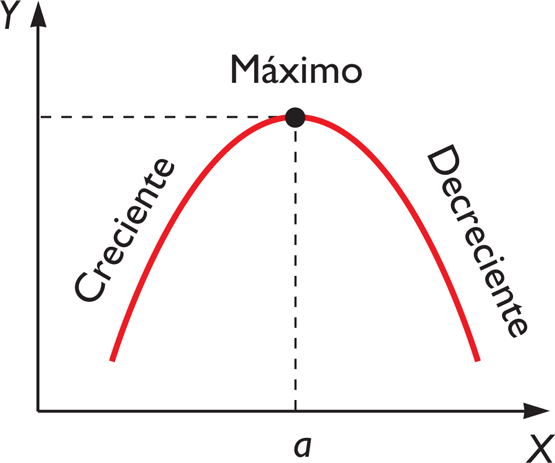
Dada una función continua en un punto x=a, se dice que presenta un máximo relativo, si a la izquierda de dicho punto la función es creciente y la derecha la función es decreciente.
Si, por el contrario, la función es decreciente a la izquierda y creciente a la derecha hay un mínimo relativo.
Si se verifica que f(a)>f(x) para cualquier valor x del dominio, y no sólo para los valores de "alrededor", se habla de máximo absoluto en x=a.
Y análogamente se dice que en x=a hay un mínimo absoluto si f(a)<(f(x) para cualquier x del dominio.
Es decir, una función f(x) tiene un máximo relativo en x=a, si existe un entorno E(a) tal que: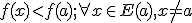 
Y una función f(x) presenta un mínimo relativo en x=a, cuando existe un entorno E(a) tal que: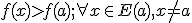 
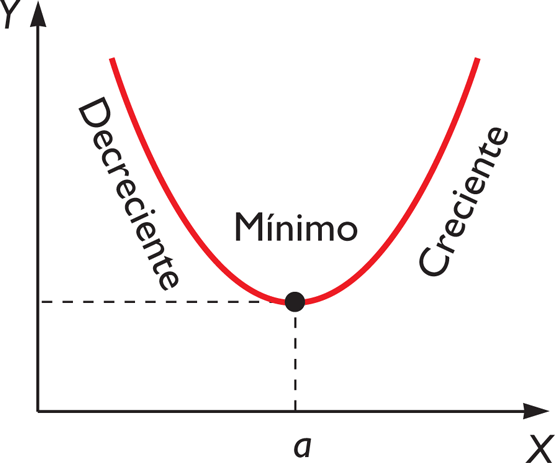
A los máximos y mínimos relativos se los llama extremos relativos o simplemente extremos.
Ejemplo o ejercicio resuelto
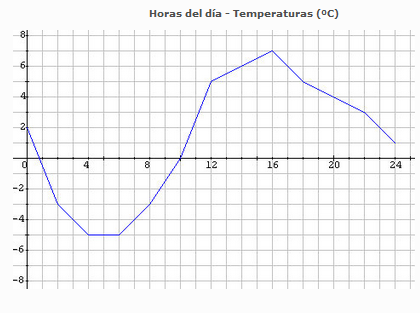
En la siguiente imagen puedes ver la gráfica de las temperaturas a lo largo de un día en una ciudad española. En el eje OX están representadas las horas del día y en el eje OY las temperaturas en grados centígrados.
