3. Más y más lejos
 |
| Imagen de Inti bajo licencia Creative Commons. |
Acabamos de ver que a veces la función se aleja y se aleja hasta irse al infinito. Si recuerdas, algo de esto vimos ya el curso pasado, más concretamente en el último tema de la unidad 3 cuando representamos las funciones racionales, ( si no te acuerdas, no te preocupes que en el siguiente tema lo vamos a repasar.)
Asíntota vertical
En ese tema, vimos que había casos en los que al acercarnos a un valor de "x", la función iba tomando valores más y más grandes. Esta es la idea de asíntota vertical, una recta vertical de forma que cuando x se acerca a ese punto, la función se va pegando a esa recta.
Observa las siguientes escenas. Mueve el punto rojo o el control P.x para hacerlo con más precisión y fíjate que mientras más nos acercamos a -2 en la primera escena o a 1 en la segunda, más se va a infinito la función.
Por tanto, en la primera escena la recta x = -2 es una asíntota vertical y en la segunda, la recta x = 1.
Applets Descartes de Antonio Caro Marchante bajo licencia Creative Commons
 |
| Imagen de bibigeek bajo licencia Creative Commons |
Asíntota horizontal
También puede ocurrir lo contrario, o sea, que a medida que nos alejemos en el valor de X, el valor de la función se vaya acercando a uno concreto. Esto ocurre con frecuencia en el ámbito de las ciencias sociales cuando un determinado proceso se estabiliza (ya no puede crecer más) o en la biología cuando una determinada población se estabiliza. La relación entre presas y predadores llega al punto en el que la población en una determinada región ni crece ni disminuye.
Fíjate en la siguiente escena. La gráfica muestra la evolución de una población de búhos en una determinada zona:
Applets Descartes de Antonio Caro Marchante bajo licencia Creative Commons
Como puedes ver desplazando el punto rojo, el número inicial de búhos va aumentando progresivamente a lo largo del tiempo (eje X) hasta que llega un momento en el que por más tiempo que transcurra, la población, no aumenta, se estabiliza en el valor 7 de esa escala.
Como ves, la gráfica de la función se pega a una recta horizontal y por eso decimos, que cuando x tiende a infinito la recta y=7 es una asíntota horizontal.
La recta x = k es una asíntota vertical, si cuando x se acerca a k, la función se va hacia el infinito.
La recta y = k es una asíntota horizontal, si cuando x se va hacia el infinito (+∞ ó -∞) el valor de la función se va aproximando a k.
En esta actividad tienes que poner las asíntotas verticales y horizontales. Para que te lo reconozca bien, escribe las asíntotas verticales, por ejemplo, x=4, sin dejar espacios en blanco y del mismo modo las horizontales. En caso de que no haya, escribe el mensaje: no
 |
 |
 |
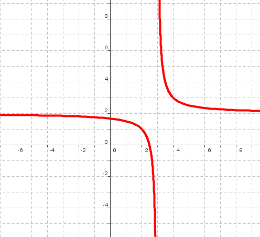
Gráfica 1
Asíntota vertical ; Asíntota horizontal en -∞ ; Asíntota horizontal en +∞
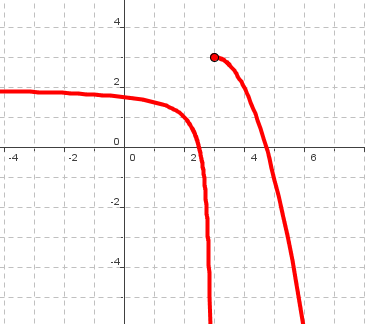
Gráfica 2
Asíntota vertical ; Asíntota horizontal en -∞ ; Asíntota horizontal en +∞
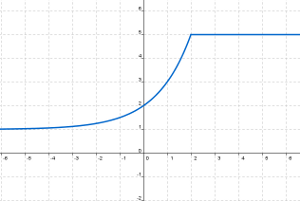
Gráfica 3
Asíntota vertical ; Asíntota horizontal en -∞ ; Asíntota horizontal en +∞