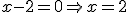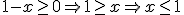1.1. Dominamos y recorremos los ejes
 |
| Imagen de Adam Solomon con licencia Creative Commons |
A la hora de diseñar la caseta de feria de TRANSVELOX, hemos decidido montar el escenario en el centro de la caseta. Queremos que sea cuadrado y tenga una extensión de entre 100 y 170 m2.
Le hemos pedido a Nacho, nuestro matemático, que nos ayude a calcular cuánto ha de medir el lado del escenario y según la medida que extensión total tendrá.
Se ha puesto manos a la obra y al cabo de dos horas nos ha citado en la sala de juntas. Allí nos ha presentado la siguiente animación:
A partir de la gráfica nos ha dado la siguiente explicación.
|
| Imagen de Oneras bajo licencia Creative Commons |
Como el escenario es cuadrado, el área total será A=l2. El área dependerá de la medida del lado, luego la función que nos da la medida del área en función del lado es y=f(l)=l2, dónde el lado l es la variable independiente y el área es la variable dependiente.
Al representar la función nos aparece la figura de la imagen. Corresponde a la gráfica de f(x)=x2, pero sólo un "trozo" de ella. Como sólo puede tomar valores entre 100 y 170 m2, esto quiere decir que los posibles valores que toma la función van de 100 a 170 en el eje Y, y por lo tanto, los posibles valores de la medida del lado son de 10 a 13 m. aproximadamente, pues 102=100 y (13,03..)2=170.
Al conjunto de los posibles valores de la variable independiente, la medida del lado, se le llama Dominio de la función. En este caso se representa en forma de intervalo: Dom f=[10,13.03].
Por otro lado, a los posibles valores de la variable dependiente, área del tablao, se le llama Recorrido de la función.
Mueve el deslizador correspondiente a la velocidad y podrás ver en la animación los valores del dominio y el recorrido.
Importante
El subconjunto de números reales "x" para los que la función está definida se llama Dominio de f, y se representa como Dom (f).
Los valores "y" que toma la imagen forman un subconjunto llamado Imagen o recorrido de f, y su representación es Rec(f).
Cuando necesitamos calcular el dominio de una función que viene expresada por su fórmula, tenemos que tener en cuenta si no se puede realizar alguna de las operaciones para ciertos valores de la variable independiente.
Por ejemplo, si tenemos a la variable afectada por una raíz cuadrada, el contenido de esta ha de ser positivo o nulo, o, si tenemos un cociente, el denominador no puede valer cero.
Ejemplo o ejercicio resuelto
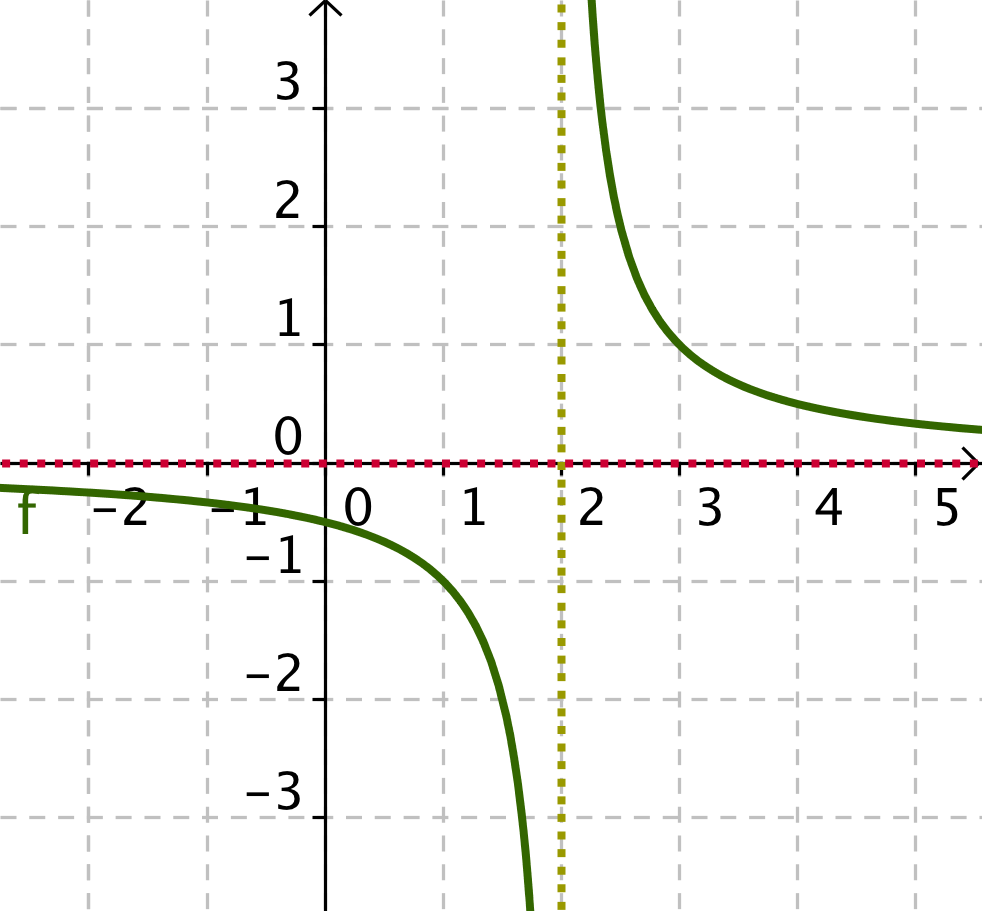
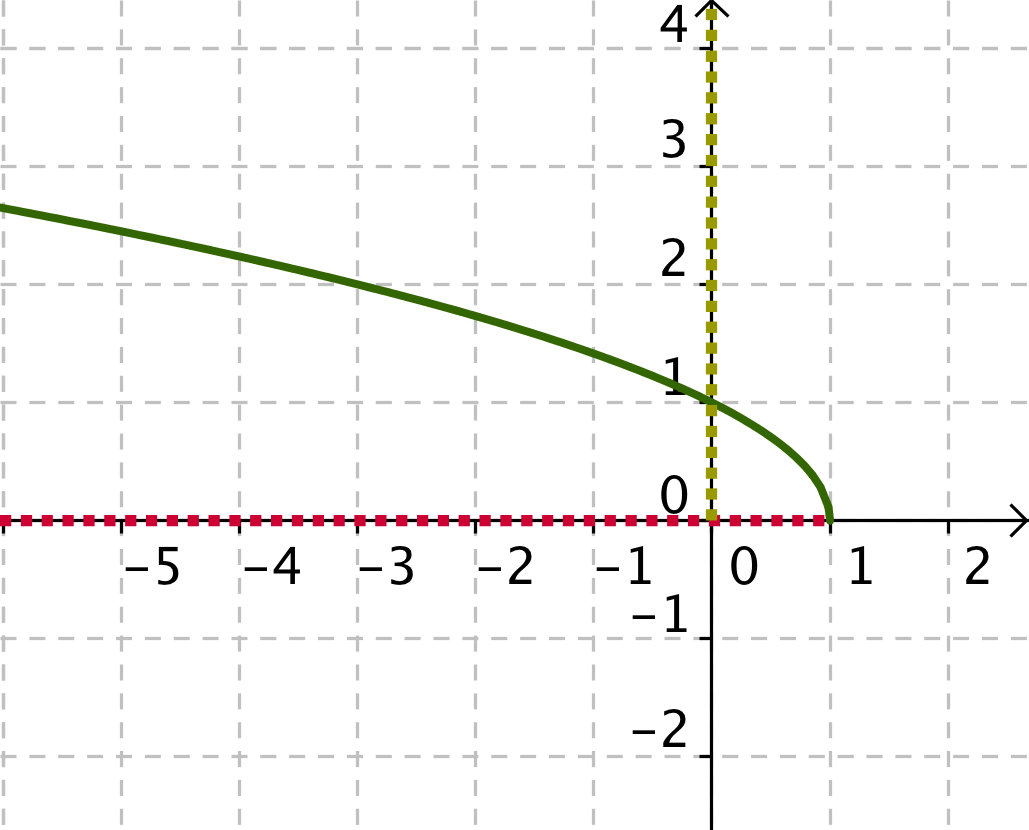
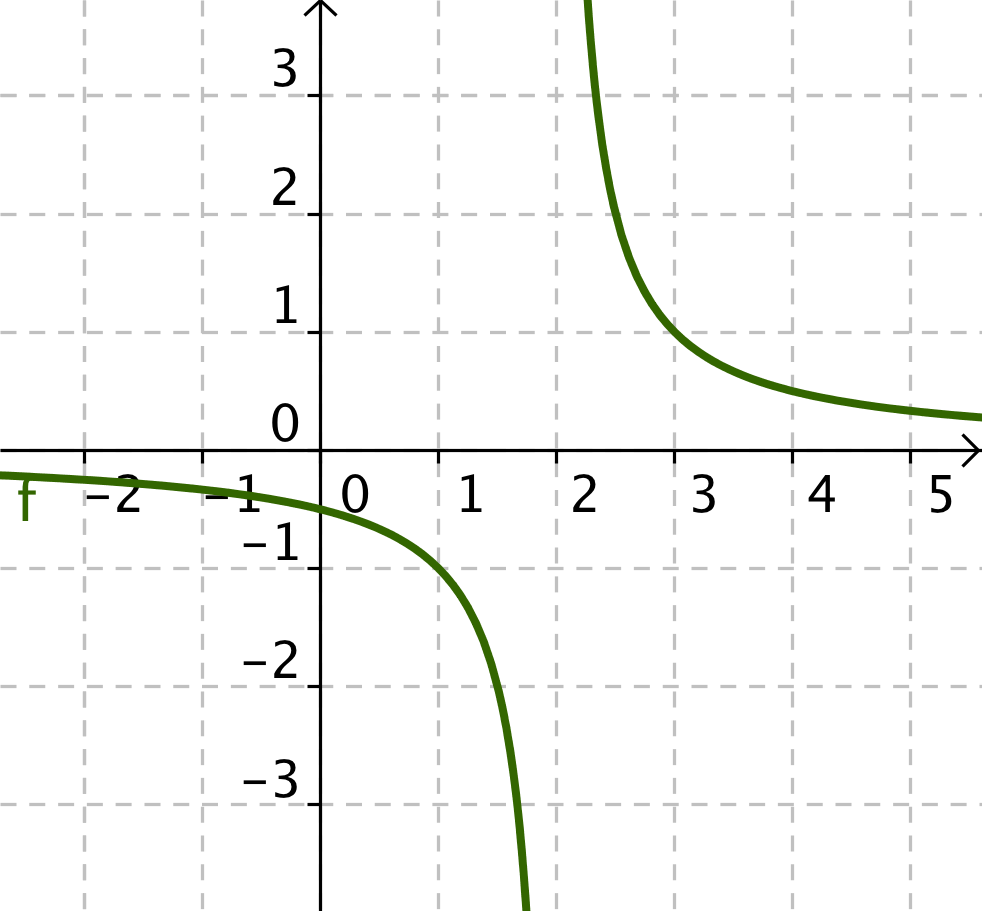
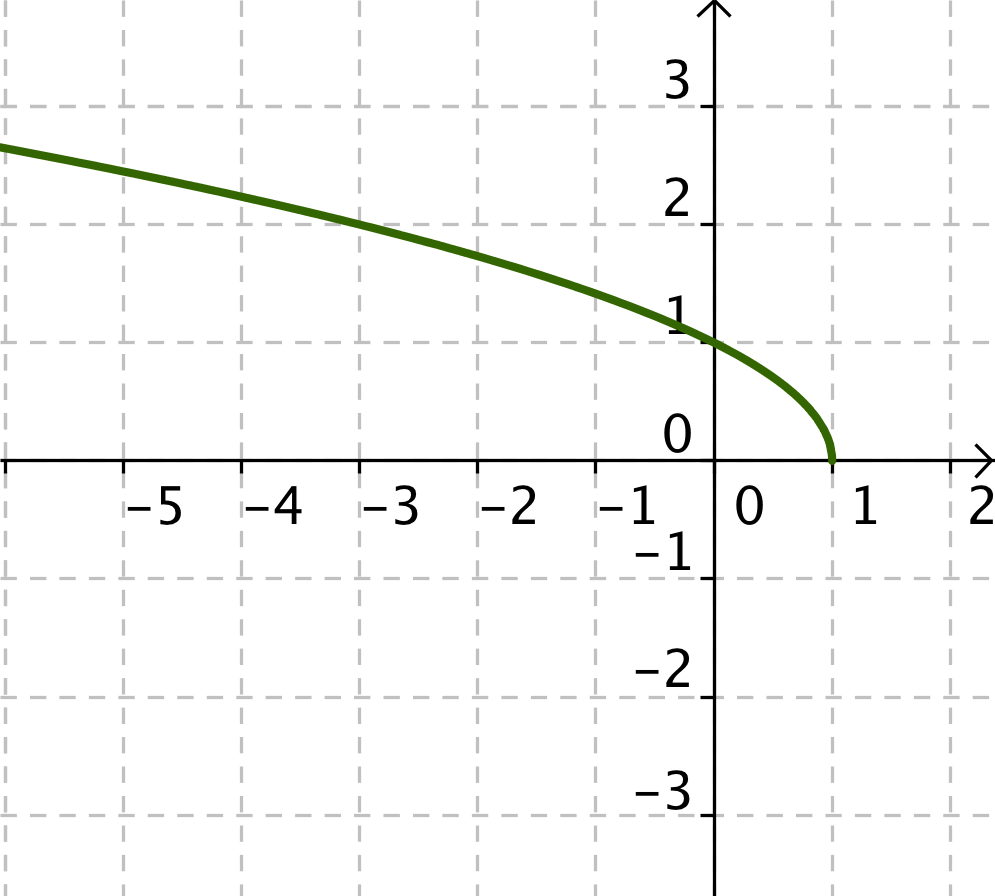
Calcular el Dominio y el recorrido de las siguientes funciones:
|
|
 |
 |
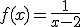
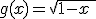
Recuerda:
- El dominio se observa sobre el eje X y recorrido sobre el eje Y
- Cuando tenemos un cociente el denominador no se puede anular.
- Si lo que tenemos es una raíz cuadrada, el radicando ha de ser positivo.
Calcular el Dominio, analíticamente, de las siguientes funciones:
AV - Reflexión
En el siguiente ejercicio tienes que averiguar el dominio de las funciones que aparecen.
Empieza por la actividad 1 y , en cada una de ellas puedes realizar más ejercicios similares pulsando sobre el botón otra función.
Applet Descartes publicado en EDAD bajo licencia Creative Commons.
Para saber más
En este vídeo puedes ver como se calcula el dominio de una función donde se combina un cociente con una raíz.