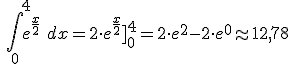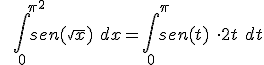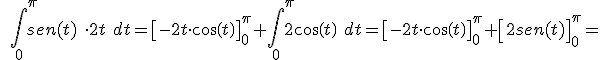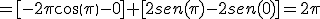1.3. La regla que usamos
 |
| Fuente propia |
Imagina que una persona aficionada a la repostería (quizás tú valgas como ejemplo) quiere hacer un pastel o un dulce que esté horneado. Para ello necesita los ingredientes y por supuesto una herramienta que le permita cocinar lo que desea. En nuestro caso deberá utilizar un horno que le permita cocinar lo que tiene en la cabeza. A nosotros nos pasa algo parecido.
Ya hemos visto cuál es la interpretación de la integral definida y hemos relacionado, en el apartado anterior, la función integral con la otra gran herramienta del cálculo infinitesimal: la derivada. Pero ahora necesitamos una herramienta que nos permita hallar el valor de la integral definida. Y para ello contamos con la Regla de Barrow.
REGLA DE BARROW
Sea f(x) una función definida en el intervalo [a,b] y sea F(x) una primitiva de dicha función. Se verifica que la integral definida, entre a y b, es igual a la diferencia de la función primitiva en los extremos del intervalo. Es decir,
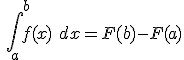
La forma de deducir esta regla es muy simple. Sabemos que la integral indefinida de una función está formada por todas sus primitivas. Es decir, es igual a una primitiva cualquiera más cualquier constante que queramos añadir. Esto lo vimos en el tema anterior. Por ello,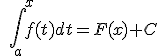
Si sustituimos x por a, obtendríamos el área limitada por la función entre ese valor y él mismo, que lógicamente es cero. Por tanto:
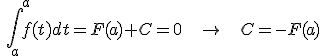
Y en 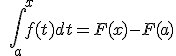 basta sustituir x por b para obtener la Regla de Barrow.
basta sustituir x por b para obtener la Regla de Barrow.
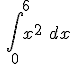 .
.
En el siguiente enlace tienes más ejercicios de integral definida resueltos utilizando la Regla de Barrow.
 .
.
a) 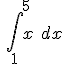 =
=
b) 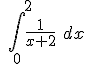 =
=
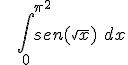
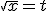 .
.
 |
| Imagen de contenido libre alojada en la página de Wikimedia Commons. |
Ya en el vídeo introductorio del tema, al hablar de los precursores del Cálculo, se citó el nombre de Isaac Barrow, matemático, profesor y teólogo inglés del siglo XVII. Fue profesor de la cátedra Lucasiana en Cambridge, cátedra que cedió en 1669 a uno de sus discípulos, Sir Isaac Newton.
Muchos historiadores consideran que podría haber descubierto el cálculo diferencial antes que Newton y Leibniz si no hubiese tenido tanto apego a los aspectos geométricos de las matemáticas.
Precisamente en 1669 publicó sus Lectiones Opticae et Geometricae en el que se presenta métodos para hallar tangentes a curvas cualesquiera y plantea que la diferenciación e integración son procesos inversos. Este libro fue revisado y corregido por el propio Newton. También publicó ediciones comentadas de libros de Euclides, Apolonio y Arquímedes, entre otros.
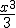 . Por lo tanto:
. Por lo tanto:
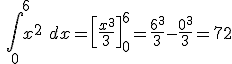
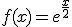 es la función
es la función 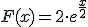 .
.