1.2. Lo fundamental
 |
| Fuente propia |
Estamos seguros de que en muchas situaciones cotidianas te has encontrado con el concepto de la media. Cuando estudias los gastos medios que has tenido en un mes o el número medio de horas que debes dedicarle a la limpieza de la casa para que esté a tu gusto, o el número medio de mensajes sms que recibes en tu móvil al año.
Si consideramos, por ejemplo, la producción de setas en la última década, seguro que tendremos un número medio anual. Ese número medio que, lógicamente, se encontrará entre la mayor producción y la menor, equivale a que si todos los años se hubiese obtenido la misma cantidad, al final de la década se tendría tanta cantidad como la obtenida en conjunto en los diez años.
Algo parecido nos va a ocurrir con la integral definida.
Consideremos una función f(x) continua en el intervalo [a,b], existe un punto c, interior al intervalo, en el que se verifica.
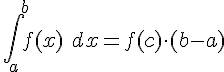
La igualdad anterior equivale a decir que el valor de la integral definida coincide con el área de un rectángulo de base la amplitud del intervalo y cuya altura es el valor de la función en el punto intermedio c.
Este resultado se conoce como TEOREMA DE LA MEDIA o del Valor Medio.
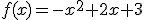 e indica en qué punto intermedio c se cumple.
e indica en qué punto intermedio c se cumple.
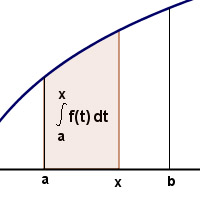 |
Si elegimos un punto x, interior al intervalo [a,b] en que está definida la función, y hallamos la integral definida entre el extremo a y ese punto x, su valor depende de ese valor x, por lo que entonces la integral definida se convierte en una función de x que recibe el nombre de Función Integral. Se suele representar por la misma letra que la función integrando, pero en mayúscula. En nuestro caso hablaremos de la función F(x) que será
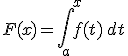
La derivada de la función integral es igual a la función integrando.
Es decir, si 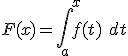 entonces
entonces 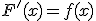 . Esto equivale a decir que la función integral es una primitiva de la función f(x).
. Esto equivale a decir que la función integral es una primitiva de la función f(x).
Este resultado se conoce como Teorema Fundamental del Cálculo.
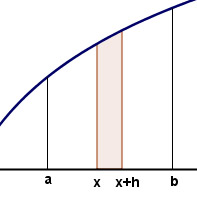 |
Lo anterior es muy fácil deducirlo utilizando el Teorema de la Media visto anteriormente. La derivada de la función F(x), según la definición, sería: 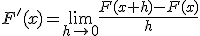 .
.
El numerador equivaldría a 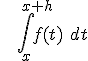 , y utilizando el Teorema del valor medio existirá un valor
, y utilizando el Teorema del valor medio existirá un valor 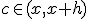 que verifica que
que verifica que 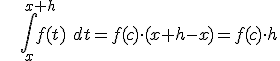 .
.
Por tanto 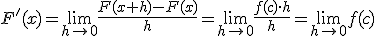 y como
y como 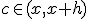 , al tender h a 0, c debe tender a x.
, al tender h a 0, c debe tender a x.
Luego obtenemos que 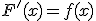 .
.