1.1. Nos vamos acercando
 |
| Foto de Luana Fischer Ferreira incluida en el Banco de Imágenes del ITE. |
En el vídeo anterior has visto un método de aproximación a una cantidad desconocida acotando por valores superiores e inferiores. Aunque creas que es algo raro la verdad es que es corriente que utilicemos cantidades aproximadas para acercarnos al valor real. Seguro que has visto muchas veces noticias en los medios sobre alguna manifestación, como la de repulsa por los atentados del 11-M que puedes ver en la imagen. Cuando se habla de la cantidad de personas que han ido a alguna de esas manifestaciones suele haber disparidad de cantidades, en algunos casos desorbitantes, pero debe de estar claro que la cantidad real de asistentes debe estar entre los valores más pequeños y otros más grandes.
Ese método de ir aproximando por valores más pequeños y más grandes recibe el nombre de exhausción y ya fue utilizado por el gran matemático Arquímedes.
Arquímedes de Siracusa fue un matemático griego que dejó para la posteridad frases muy famosas como "Eureka, lo encontré" o "Dadme un punto de apoyo y moveré el mundo". En el siguiente vídeo puedes ver algunos datos sobre su vida y parte de su impresionante legado científico.
El procedimiento que vamos a utilizar es aproximar el área que queremos medir mediante rectángulos que son, por un lado menores, y por otro mayores que el valor buscado. Algo parecido al acercamiento a la superficie de la piscina que vimos en el vídeo del apartado anterior.
Iremos dividiendo el intervalo, en el que queremos encontrar el área, en partes iguales y en ellas calcularemos la suma de áreas de rectángulos inferiores y superiores a la función en ese intervalo. En la siguiente ventana interactiva puedes apreciar cuánto va variando esa suma de intervalos a medida que vamos aumentando el número de ellos. Para verlo sólo tienes que aumentar el valor del contador n.
Si tenemos una función f(x) definida en un intervalo [a,b] podemos construir los rectángulos inferiores y superiores, tal como hemos visto en el caso anterior. En ese caso, las sumas de las áreas de los rectángulos reciben el nombre de suma inferior y suma superior de Riemann. Y se verifica que si hallamos el límite de esas sumas, es decir, el valor hacia el que tienden a medida que el número de rectángulos tiende a infinito, ambos límites coinciden y su valor recibe el nombre de Integral Definida de la función f(x) entre los valores a y b. Se suele representar por la expresión:
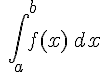

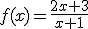 . ¿Hacia qué valor tiende la integral definida en el intervalo [0,3]?
. ¿Hacia qué valor tiende la integral definida en el intervalo [0,3]?
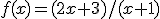 .
.