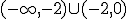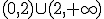2.2. El difuminado
Otro de los aspectos que nos va a ayudar a realizar la representación gráfica de una función es conocer la monotonía, es decir, sus intervalos de crecimiento y de decrecimiento. Si pulsas en la siguiente ventana te recordará cómo se hace:
|
|
Consideramos la siguiente función racional: 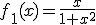
Perseguimos realizar la representación gráficamente esta función. Para ello, en esta ocasión te pedimos que estudies la monotonía de la misma.
 |
Andrés tiene en sus manos ahora los cuatro folios correspondientes al estudio sobre el crecimiento y decrecimiento de cada una de las funciones. Recuerda que las funciones que Ángela había investigado eran:
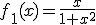 |
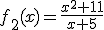 |
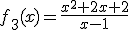 |
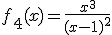 |
Ayuda a Ándrés a identificar la función a la que corresponde cada uno de los folios. Para ello completa los espacios en blanco que aparecen seguidamente.
.- El folio que indica que la función es creciente en el intervalo 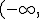
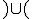 1
1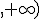 y decreciente en el intervalo (
,
y decreciente en el intervalo (
,
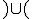 ,
) corresponde a la función
.
,
) corresponde a la función
.
.- El folio que indica que la función es creciente en el intervalo 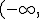
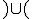
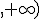 y decreciente en el intervalo (
,
y decreciente en el intervalo (
,
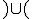 ,
) corresponde a la función
.
,
) corresponde a la función
.
.- El folio que indica que la función es creciente en el intervalo (
,
) y decreciente en el intervalo 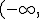
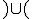
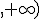 corresponde a la función
.
corresponde a la función
.
.- El folio que indica que la función es creciente en el intervalo 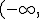
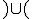 ,
,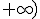 y decreciente en el intervalo (
,
) corresponde a la función
.
y decreciente en el intervalo (
,
) corresponde a la función
.
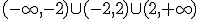
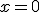 .
.
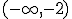
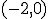
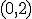
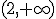
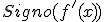
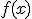 es decreciente en
es decreciente en