3. Trabajando otras técnicas
Representa gráficamente las siguientes funciones polinómicas:
a) 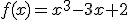
b)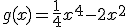
Representa gráficamente la siguiente función:
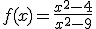
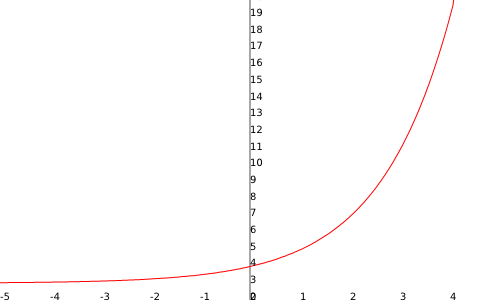
Ahora vamos a aplicar lo aprendido para representar funciones logarítmicas y exponenciales. En la siguiente ventana interactiva puedes recordar lo que conoces de la función exponencial y la logarítmica que te pueden ayudar a representarlas gráficamente:
|
|
Las matemáticas pueden servir para atajar la expansión de los virus. Según algunos científicos, las infecciones por gripe común podrían reducirse del 34% al 5% de la población si se usan modelos matemáticos a la hora de distribuir las vacunas. De momento, son modelos en un papel, pero puede que, en no mucho tiempo, sean la herramienta perfecta para frenar el avance de los virus.
|
|
En un estudio epidemiológico, al utilizar un modelo matemático, el número de casos que se evitaba contagiar según los cálculos se correspondía con la función 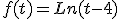 .
.
Donde 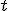 es el tiempo transcurrido en horas desde que se comienza a vacunar al primer individuo. Para conocer más a fondo los efectos de este modelo, los ciéntíficos necesitan representar gráficamente la función anterior. Ayúdales realizando los cálculos oportunos para obtener la información necesaria para representarla.
es el tiempo transcurrido en horas desde que se comienza a vacunar al primer individuo. Para conocer más a fondo los efectos de este modelo, los ciéntíficos necesitan representar gráficamente la función anterior. Ayúdales realizando los cálculos oportunos para obtener la información necesaria para representarla.
En un laboratorio han creado un cultivo bacteriológico y han observado su crecimiento. El cultivo lo comenzaron con 4 bacterias. Tres de ellas murieron enseguida y no sufrieron ninguna transformación. La cuarta sin embargo se dividió en dos cuando había pasado un minuto. Esas dos se volvieron a dividir en dos cada una de ellas cuando había pasado otro minuto. Y así se iban dividiendo sucesivamente. Cada vez que pasaba un minuto las bacterias que había en el cultivo se dividían en dos excepto las tres que habían muerto al principio. Algo parecido a lo que puedes observar en el siguiente vídeo.
|
|
Los investigadores quieren hacer un estudio sobre este cultivo, para ello han decidido comenzar con un estudio matemático del comportamiento del mismo. Lo primero que desean hacer es encontrar la función que les proporcione el número de bactrias que hay en el cultivo en función del tiempo transcurrido desde que echaron las 4 primeras. Y lo segundo que quieren hacer es representar gráficamente esa función de forma que se puedan hacer una idea gráfica de lo que sucede en el cultivo. ¿Puedes ayudarles?
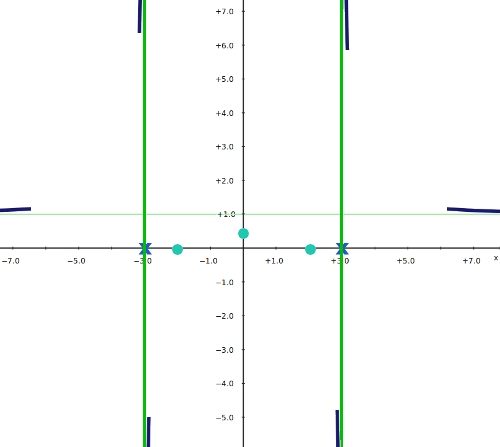
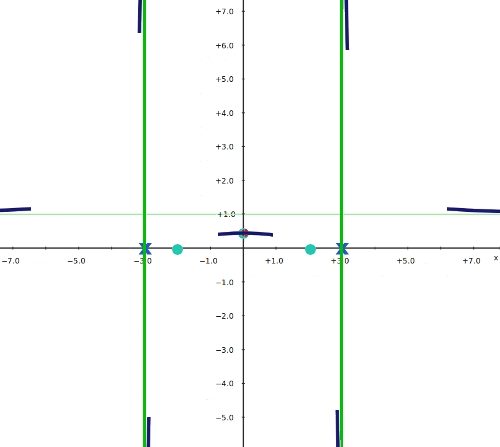
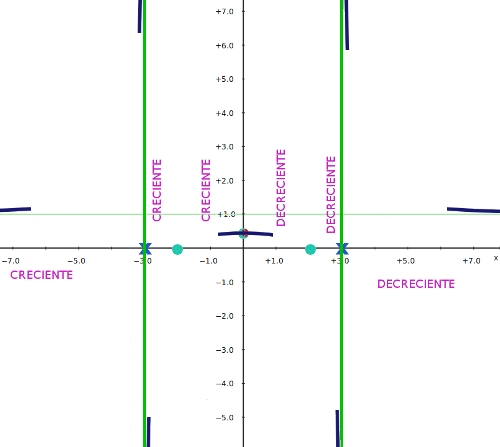
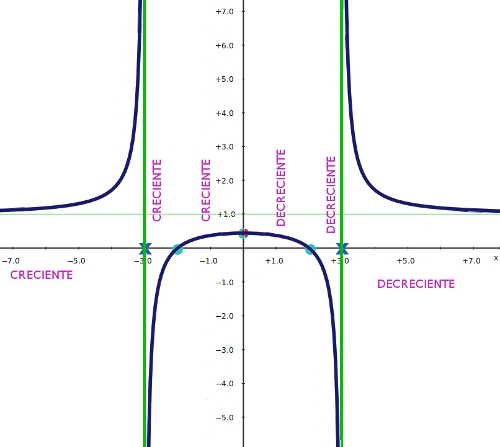
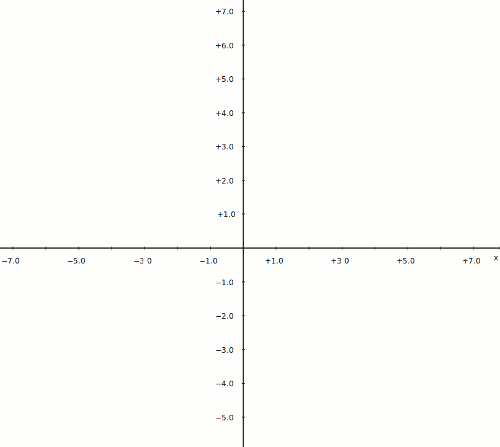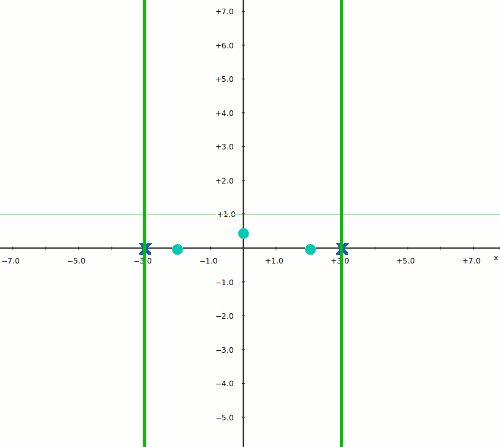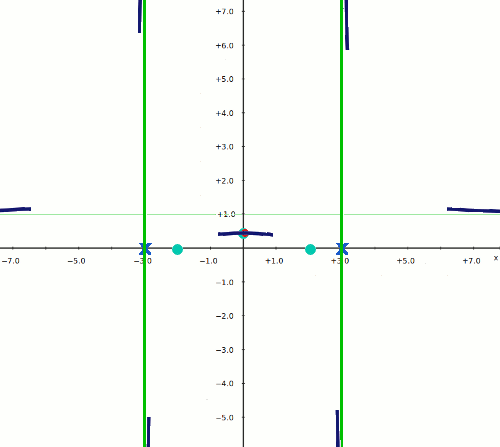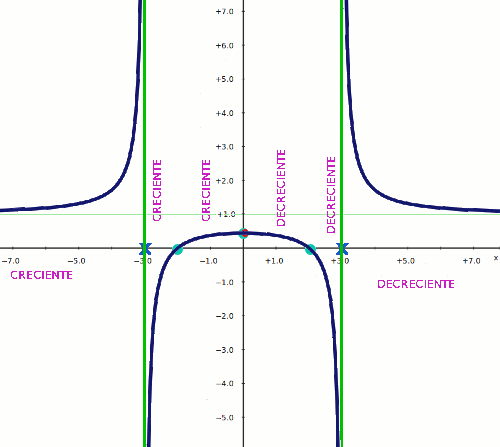
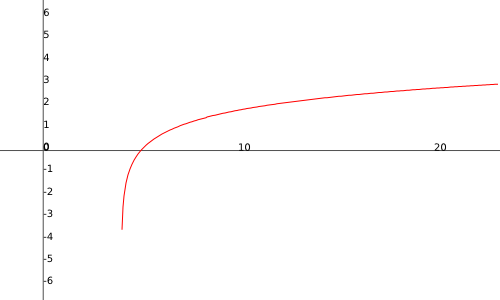
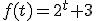 donde
donde