2.1. La curvatura es la que manda
 |
| Fuente propia |
Seguro que tienes la sensación de que a veces el tiempo pasa muy rápido y otras veces, sin embargo, los tiempos de espera se nos hacen eternos. Algún listo diría que el tiempo es relativo, pero es que el ser relativo es algo bastante corriente.
Suele ocurrir que no siempre se crece o decrece con la misma intensidad. Por ejemplo, imagina que un programa de radio abre un apartado en Facebook para que los seguidores de ese programa se hagan amigos en dicha red social. Al principio el aumento de amigos será muy rápido, pero a medida que va pasando el tiempo el aumento cada vez será más lento. Esto pasa en muchas situaciones de la vida y, por supuesto, también en las funciones.
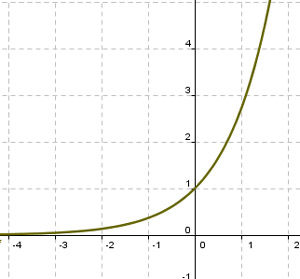
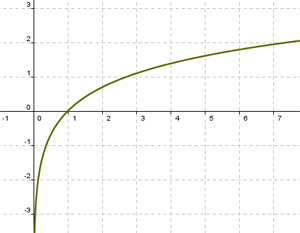
En temas anteriores has trabajado con dos funciones concretas, la exponencial y la logarítmica. Observa en las gráficas siguientes el crecimiento de ambas funciones. En la exponencial al principio se aumenta lentamente hasta llegar al valor x=0 y después comienza a aumentar mucho más rápidamente. En la logarítmica es al revés. Hasta el punto x=1 aumenta muy rápidamente y después sigue aumentando pero cada vez de una forma más lenta. Eso es debido a que las dos funciones tienen distinta curvatura.
 |
 |
La curvatura de una función estudia la forma en que esa función se curva y se mide por su relación con la tangente. Hay dos tipos de curvatura.
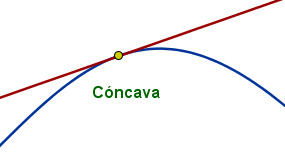
Una función se dice que es cóncava en un punto si al trazar la tangente a la función en dicho punto, la función queda por debajo de la tangente en los alrededores de ese punto.
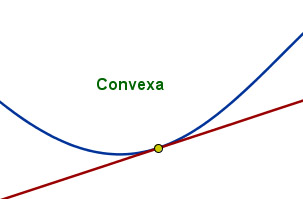
Una función se dice que es convexa en un punto si al trazar la tangente a la función en dicho punto, la función queda por encima de la tangente en los alrededores de ese punto.
 |
 |
Si no puedes ver la anterior escena pulsa sobre el siguiente enlace.
Si tenemos una función que admite, al menos, hasta la segunda derivada en un punto x=a tenemos el siguiente resultado.
- Si
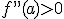 , la función es convexa en el punto a.
, la función es convexa en el punto a. - Si
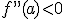 , la función es cóncava en x=a.
, la función es cóncava en x=a.
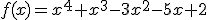 .
.
 |
| Fotografía tomada del Banco de Imágenes del ITE. |
En un invernadero se está realizando el estudio del crecimiento de un nuevo tipo de planta. Es interesante estudiar cuando crece más y cuando menos, por ello, los científicos quieren estudiar la curvatura de la función que han aproximado al crecimiento de la planta en las primeras semanas. Esa función viene dada por la expresión
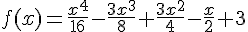
Ayúdales hallando los intervalos de concavidad y convexidad de esa función.
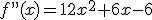 .
.
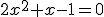 .
.
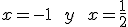 . Estudiamos el signo de la segunda derivada en los intervalos que nos indican esos valores.
. Estudiamos el signo de la segunda derivada en los intervalos que nos indican esos valores.
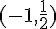 y convexa en
y convexa en 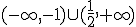 .
.
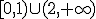 y convexa en el intervalo
y convexa en el intervalo 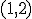 .
.