3. Especial Selectividad
Sea 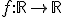 la función definida por
la función definida por 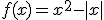 .
.
a) Estudia la derivabilidad de f.
b) Determina los intervalos de crecimiento y decrecimiento de f.
c) Calcula los extremos relativos de f (puntos donde se alcanzan y valor de la función).
Sea la función 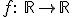 definida por
definida por 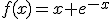 .
.
a) Determina los intervalos de crecimiento y de decrecimiento de f, así como los extremos relativos o locales de f.
b) Determina los intervalos de concavidad y convexidad de f.
Sea 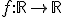 la función definida por
la función definida por 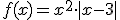 .
.
a) Estudia la continuidad y derivabilidad.
b) Estudia el crecimiento y decrecimiento de f. Calcula sus extremos relativos (abscisas donde se obtienen y valores que se alcanza).
Sea 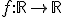 la función definida por
la función definida por 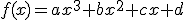 . Calcula los valores a, b, c y d sabiendo que f verifica:
. Calcula los valores a, b, c y d sabiendo que f verifica:
- El punto (0,1) es un punto de inflexión.
- f tiene un mínimo local en el punto de abscisa x=1.
- La recta tangente a la gráfica de f en el punto de abscisa x=2 tiene pendiente 1.
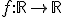 sabiendo que su derivada viene dada por
sabiendo que su derivada viene dada por 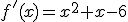 y que el valor que alcanza f en su punto de máximo (relativo) es el triple del valor que alcanza en su punto de mínimo (relativo).
y que el valor que alcanza f en su punto de máximo (relativo) es el triple del valor que alcanza en su punto de mínimo (relativo).
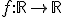 definida por
definida por 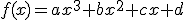 tiene extremos relativos en (0,0) y (2,2). Calcula a, b, c y d.
tiene extremos relativos en (0,0) y (2,2). Calcula a, b, c y d.
Sea 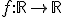 la función definida por
la función definida por 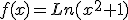 , siendo Ln la función logaritmo neperiano.
, siendo Ln la función logaritmo neperiano.
a) Determina los intervalos de crecimiento y decrecimiento y los extremos relativos de la función f.
b) Calcula la ecuación de la recta tangente a la gráfica de f en el punto de inflexión de abscisa negativa.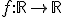 la función definida por
la función definida por 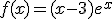 .
.
a) Calcula los extremos relativos de f (puntos donde se obtienen y valores que se alcanzan).
b) Determina la ecuación de la recta tangente a la gráfica de f en su punto de inflexión.
Sea 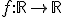 la función definida por
la función definida por 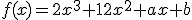 . Determina a y b sabiendo que la recta tangente a la gráfica de f en su punto de inflexión es la recta
. Determina a y b sabiendo que la recta tangente a la gráfica de f en su punto de inflexión es la recta 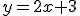 .
.
Los valores pedidos son a= y b= .
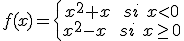
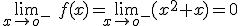 y
y 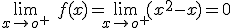 .
.
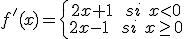
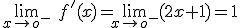 y
y 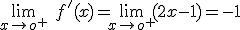 .
.
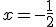 y en el segundo en
y en el segundo en 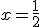 .
.
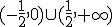 y decreciente en
y decreciente en 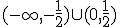 .
.
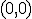 y dos mínimos relativos en
y dos mínimos relativos en 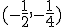 y
y 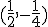 .
.
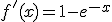 , que se anula en
, que se anula en 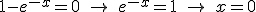
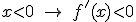 por lo tanto la función es decreciente en
por lo tanto la función es decreciente en 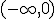 . Para los restantes valores, si
. Para los restantes valores, si 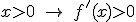 y, por eso, en el intervalo
y, por eso, en el intervalo 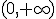 la función es creciente.
la función es creciente.
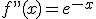 y como la función exponencial siempre es positiva, la segunda derivada siempre es positiva y por tanto la función siempre es convexa.
y como la función exponencial siempre es positiva, la segunda derivada siempre es positiva y por tanto la función siempre es convexa.
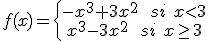 .
.
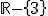 .
.
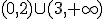 y decreciente en
y decreciente en 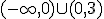 .
.
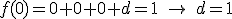 .
.
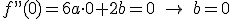 .
.
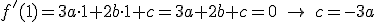 .
.
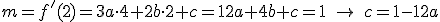 .
.
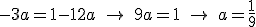 y por tanto,
y por tanto, 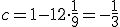 .
.
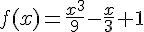
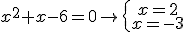 .
.
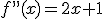 y entonces
y entonces 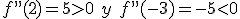 . Por tanto, en x=-3 tenemos el máximo y en x=2 el mínimo.
. Por tanto, en x=-3 tenemos el máximo y en x=2 el mínimo.
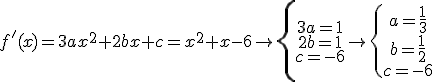
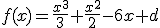 que debe cumplir la igualdad
que debe cumplir la igualdad 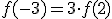 .
.
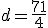 .
.
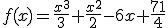 .
.
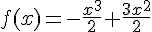 .
.
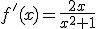 . El signo sólo depende de x, pues el denominador es siempre positivo. Por tanto, la función es creciente en
. El signo sólo depende de x, pues el denominador es siempre positivo. Por tanto, la función es creciente en 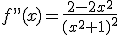 , que se anula en x=1 y en x=-1.
, que se anula en x=1 y en x=-1.
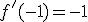 , luego la tangente en el punto
, luego la tangente en el punto 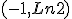 es
es 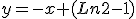 .
.
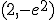 .
.
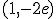 y la tangente en ese punto es
y la tangente en ese punto es 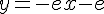 .
.