1.2. Los puertos de categoría
 |
A veces estamos realizando alguna labor en el trabajo o en casa y de pronto tenemos la sensación de que nos olvidamos de algo. ¿No te ha ocurrido nunca? Por ejemplo, estamos preparando la maleta para salir de viaje y tenemos la impresión que hay algo que nos va a hacer falta y que no hemos echado.
Si piensas en lo que hemos visto en el apartado anterior, ¿no tienes esa sensación? Hemos dicho que si la derivada es positiva la función es creciente y es negativa es decreciente, pero ¿qué pasa si la derivada vale cero? Pues la respuesta es que depende, como vamos a ver en este apartado.
Antes recordemos la definición de los extremos relativos y absolutos de una función que vimos en el primer tema de la Unidad 4.
 |
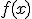 tiene un máximo relativo en el punto
tiene un máximo relativo en el punto 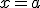 si en todos los valores próximos a este punto, el valor de la función es más pequeño que
si en todos los valores próximos a este punto, el valor de la función es más pequeño que  o lo que es lo mismo, hasta el valor
o lo que es lo mismo, hasta el valor  la función es creciente y después de este valor la función es decreciente.
la función es creciente y después de este valor la función es decreciente.
Si para todos los valores 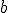 se cumple que
se cumple que 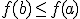 , entonces se dice que tiene un máximo absoluto en
, entonces se dice que tiene un máximo absoluto en 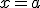 .
.
Si tenemos una función 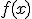 tiene un mínimo relativo en el punto
tiene un mínimo relativo en el punto 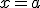 si en todos los valores próximos a este punto, el valor de la función es más grande que
si en todos los valores próximos a este punto, el valor de la función es más grande que  o lo que es lo mismo, hasta el valor
o lo que es lo mismo, hasta el valor  la función es decreciente y después de este valor la función es creciente.
la función es decreciente y después de este valor la función es creciente.
Si para todos los valores 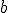 se cumple que
se cumple que 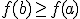 , entonces se dice que tiene un mínimo absoluto en
, entonces se dice que tiene un mínimo absoluto en 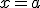 .
.
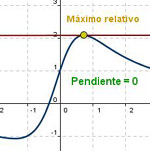 |
Si una función tiene un extremo relativo en el punto x=a y, en él, existe la derivada, entonces se cumple que 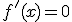 .
.
Los puntos que anulan la primera derivada reciben el nombre de puntos críticos y, entre ellos, pueden estar los extremos relativos de una función.
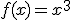 siempre es creciente, mientras mayor es x mayor es la función, por tanto, no tiene extremos. Sin embargo, su derivada en el punto x=0 vale cero. Por ello vamos a ampliar las condiciones anteriores con nuevos datos.
siempre es creciente, mientras mayor es x mayor es la función, por tanto, no tiene extremos. Sin embargo, su derivada en el punto x=0 vale cero. Por ello vamos a ampliar las condiciones anteriores con nuevos datos.
Si la función 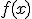 tiene derivada nula en el punto x=a,
tiene derivada nula en el punto x=a, 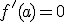 , y existe la segunda derivada en dicho punto se cumple:
, y existe la segunda derivada en dicho punto se cumple:
- Si
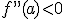 entonces la función tiene un máximo relativo en x=a.
entonces la función tiene un máximo relativo en x=a. - Si
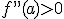 , entonces en x=a la función alcanza un mínimo relativo.
, entonces en x=a la función alcanza un mínimo relativo.
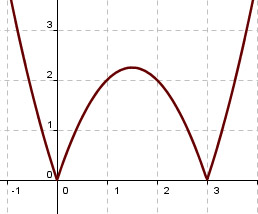 |
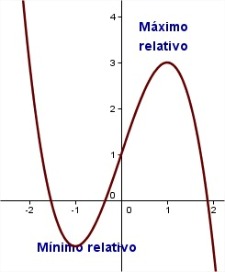
Como puedes observar seguimos dejándonos casos atrás, porque en lo anterior no se dice nada sobre qué ocurre si 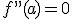 . Además puede haber funciones que tengan extremos relativos y su derivada primera no se anule porque no exista la derivada de la función en ese punto. Por ejemplo, eso le ocurre a la función
. Además puede haber funciones que tengan extremos relativos y su derivada primera no se anule porque no exista la derivada de la función en ese punto. Por ejemplo, eso le ocurre a la función 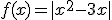 en los puntos en los que tiene mínimos relativos, como puedes apreciar en la imagen.
en los puntos en los que tiene mínimos relativos, como puedes apreciar en la imagen.
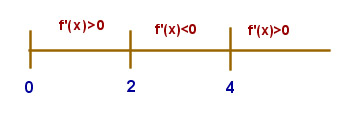
Por ello lo más comodo, en general, es estudiar el signo de la primera derivada, en aquellos puntos en los que exista la función, y tener presente las siguientes definiciones:
- Una función alcanza un máximo relativo en un punto si en él pasa de ser creciente a ser decreciente.
- En el punto x=a tendremos un mínimo relativo si en él la función pasa de ser decreciente a ser creciente.
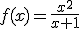 .
.
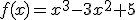 , interesa saber donde están los extremos relativos pues suelen coincidir con lugares en los que se instalan luces ambientales.
, interesa saber donde están los extremos relativos pues suelen coincidir con lugares en los que se instalan luces ambientales.
El máximo absoluto se consigue en el punto ( , ).
El mínimo absoluto corresponde al punto ( , ).
 |
| Foto obtenida del Banco de Imágenes del ITE. |
En el estudio del funcionamiento de una bomba inyectora se ha estudiado el grado de calentamiento que alcanza según el tiempo en que está funcionando, obteniendose la función siguiente.
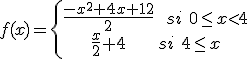
Queremos estudiar en qué momentos alcanzan extremos relativos.
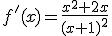 y habíamos estudiado que se anula en x=0 y en x=-2. Hallamos la segunda derivada.
y habíamos estudiado que se anula en x=0 y en x=-2. Hallamos la segunda derivada.
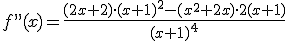
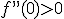 y por tanto tenemos un mínimo relativo en el punto (0,0). (Recuerda que para obtener la segunda componente siempre se sustituye el valor de x en la función, no en las derivadas).
y por tanto tenemos un mínimo relativo en el punto (0,0). (Recuerda que para obtener la segunda componente siempre se sustituye el valor de x en la función, no en las derivadas).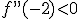 y por ello en el punto (-2-4) tenemos un máximo relativo.
y por ello en el punto (-2-4) tenemos un máximo relativo.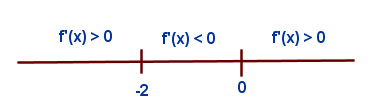
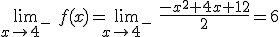 y
y 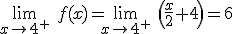
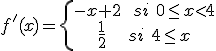
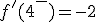 y
y 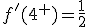 .
.