1.1. Subir y bajar sin descanso
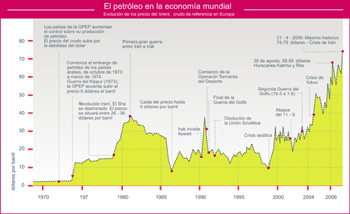 |
| Ilustración de Alejandro Cana Sánchez tomada del Banco de Imágenes del ITE. |
Cuando estamos estudiando cualquier parámetro social que utilicemos en nuestra vida cotidiana no es raro que nos importe cuando esos elementos suben o bajan, pues esas variaciones indican si la situación mejora o empeora. Además, depende del estudio que realicemos unas veces será buena idea y otras no. Por ejemplo, no es lo mismo que suba el número de las personas inscritas en el paro que las inscritas en la Seguridad Social. En el gráfico adjunto podemos ver la evolución de los precios del petróleo en un margen de más de 35 años y vemos fácilmente los momentos en que ha sido creciente y cuando no el precio.
Vamos a ver como las derivadas nos ayudan a acotar esos momentos. Antes vamos a recordar la definición de función creciente y decreciente.
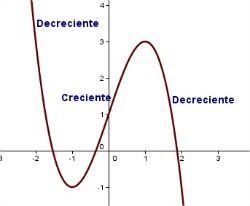 |
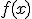 decimos que es creciente si al dibujar su gráfica de izquierda a derecha el trazo cada vez es más alto. Por tanto, es creciente si al tomar dos valores
decimos que es creciente si al dibujar su gráfica de izquierda a derecha el trazo cada vez es más alto. Por tanto, es creciente si al tomar dos valores  y
y 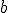 cualesquiera, si
cualesquiera, si 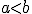 entonces
entonces 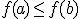 .
.
Si tenemos una función 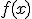 decimos que es decreciente si al dibujar su gráfica de izquierda a
derecha el trazo cada vez es más bajo. Por tanto, es decreciente si al
tomar dos valores
decimos que es decreciente si al dibujar su gráfica de izquierda a
derecha el trazo cada vez es más bajo. Por tanto, es decreciente si al
tomar dos valores  y
y 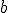 cualesquiera, si
cualesquiera, si 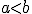 entonces
entonces 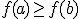 .
.
Lo más normal es que la función no sea siempre creciente o decreciente, sino que se alternen los intervalos de crecimiento y de decrecimiento.
Si no ves la escena correctamente, pulsa aquí.
A partir de lo anterior podemos deducir lo siguiente.
Si la función f(x) verifica en un punto x=a que su derivada es positiva, 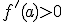 , la función es creciente en dicho punto.
, la función es creciente en dicho punto.
De forma análoga, si la derivada es negativa, 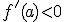 , la función es decreciente en x=a.
, la función es decreciente en x=a.
Por lo tanto, basta estudiar los intervalos en los que la función derivada es positiva o negativa para saber cuando es creciente o decreciente.
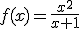 .
.
 |
| Fotografía tomada del Banco de Imágenes del ITE. |
A veces, contactan con la empresa de Ángela y Andrés para que se encarguen del estudio de una parte de un proyecto más grande. Eso les ocurrió cuando se construyó la nueva terminal del aeropuerto de Barajas en Madrid: la T4.
Le pidieron que hicieran un estudio sobre el recorrido de las brisas creadas por los aires acondicionados en lo que iban a ser los techos de la terminal. Para ello tenían que estudiar los intervalos de crecimiento y decrecimiento de la función que, inicialmente, iban a seguir las volutas del techo. La función se acercaba a la de expresión 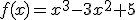 . Halla los intervalos en los que crece y decrece.
. Halla los intervalos en los que crece y decrece.
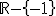 .
.
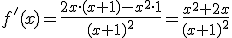 .
.
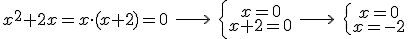 . Basta ahora estudiar el signo de la derivada en los intervalos que nos indican esos valores. La forma más rápida es darle valores a la derivada y estudiar su signo. Debemos recordar que en el punto -1 la función no existe.
. Basta ahora estudiar el signo de la derivada en los intervalos que nos indican esos valores. La forma más rápida es darle valores a la derivada y estudiar su signo. Debemos recordar que en el punto -1 la función no existe.
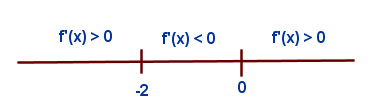
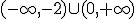 .
.
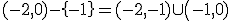 .
.
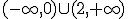 y decreciente en el intervalo
y decreciente en el intervalo 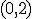 .
.