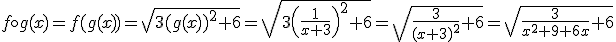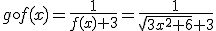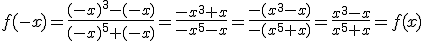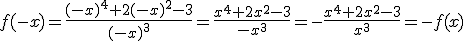1.2. Barajando funciones
 |
| Baraja, imagen obtenida del banco de imágenes del ITE |
Si tenemos dos funciones cualesquiera podemos efectuar con ellas las mismas operaciones que realizamos con los números: suma, resta, multiplicación y división. Podemos obtener también una potencia de la función, su raíz cuadrada, su logaritmo... Al realizar cualquiera de estas operaciones se vuelve a obtener otra función, pero ojo, lo más normal es que el dominio de la función resultante sea distinto del dominio de las funciones implicadas, por lo que habría que calcularlo. Así, si tenemos las funciones
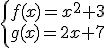podemos calcular la función
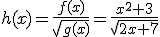. Calcula el dominio de cada una de ellas y comprueba lo que te hemos indicado sobre el dominio.
Importante
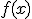y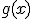 
se define la función compuesta 
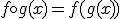. Debemos tener en cuenta que la función resultante es distinta a 
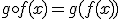. Veámoslo con un ejercicio.
Ejemplo o ejercicio resuelto
Dadas las funciones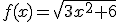 
y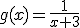 
calcula las funciones 
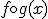y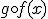 
Observa en el cuadro interactivo que se encuentra más abajo que las gráficas de las funciones 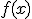, , 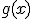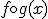y 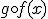son distintas. Para ello selecciona la función y pulsa sobre el botón "Mostrar ejemplo".
En el siguiente cuadro te ofrecemos una ventana interactiva que también vas a encontrar más adelante y cuyo funcionamiento es bastante sencillo. En la parte superior aparece un botón llamado "Mostrar ejemplo". Cuando lo pulses representará la función que has seleccionado a la derecha de este botón. Si quieres representar gráficamente una función deberás escribirla antes en la zona inferior, donde aparece f(x)=
Una vez escrita la función debes pulsar sobre el botón "Función nueva". En la zona derecha puedes configurar el valor máximo y mínimo que aparecerá del eje de abcisas (x) y el valor máximo y mínimo que aparecerá en el eje de la ordenada (y). Además, en la zona inferior puedes darle valores a la variable x y comprobar el valor que toma la función.
A la hora de representar una función debes tener en cuenta la forma de escribirla, así, algunas de las más utilizadas se escriben de la siguiente forma:
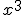=x^3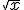 
=sqrt(x) 
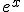=e(x)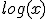 
=log(x) 
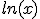=ln(x)
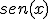=sen(x) 
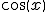=cos(x) 
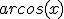=arccos(x) 
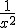= 1/(x^2)
Además, si estás viendo una gráfica y trazas un rectángulo con el ratón mientras pulsas el botón izquierdo del mismo, en la pantalla aparece ampliada esa zona. esta aproximación a un trozo de la función la puedes realizar sucesivamente para observar mejor lo que sucede en un entorno próximo. Para obtener un manual más detallado pulsa aquí.
|
Applet interactiva obtenida de la aplicación "Patrimonio Matemático de los Pueblos" de Mariano Real Pérez. Contenido interactivo del ITE. Para obtener un manual detallado pulsa aquí. |
Importante
Si tenemos una función 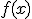diremos que es simétrica respecto al eje de ordenadas si cumple que 
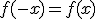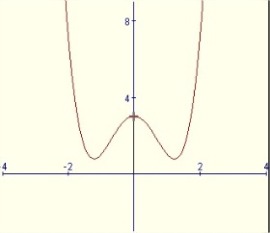
para todos los valores que pueda tomar la variable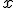 
. Gráficamente, la propiedad anterior se traduce en su gráfica en que podemos observar que a ambos lados del eje de ordenadas aparece representada la misma función pero de forma simétrica. Este tipo de funciones se dice que son pares.
 |
 |
 |
 |
Ejemplo o ejercicio resuelto
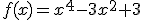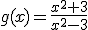Comprueba que la función
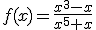es simétrica. Represéntala gráficamente en la ventana interactiva que se encuentra más arriba.
Importante
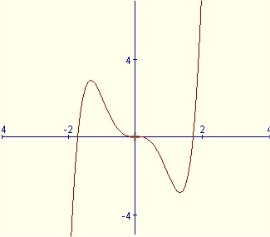
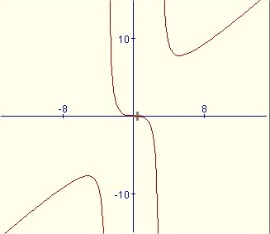
Si tenemos una función 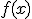diremos que es simétrica respecto al origen de coordenadas (punto (0,0)) si cumple que para todos los valores que pueda tomar la variable 
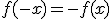. Gráficamente, la propiedad anterior se traduce en su gráfica en que podemos observar que el punto (0,0) divide a la gráfica en dos partes simétricas respecto a este punto. Este tipo de funciones se dice que son impares.
 |
 |
 |
 |
Ejemplo o ejercicio resuelto
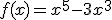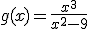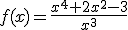es simétrica respecto al origen de coordenadas, es decir, es una función impar. Reperséntala gráficamente en la ventana interactiva que has utilizado antes.
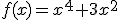
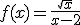
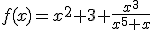
AV - Actividad de Espacios en Blanco
|
|
|
|
|
|