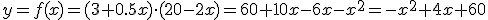1.3. La función cuadrática.
 |
| 2. Foto de frennlareo bajo licencia Creative Commons |
Ya vamos viendo una función cuya gráfica podemos encontrar con facilidad, ¿a que sí? La dificultad estriba en que normalmente la función no suele aparecer de una forma tan artificiosa como hemos visto en el apartado anterior.
Recordarás que al principio del tema dijimos que la función que íbamos a estudiar aquí no se diferenciaba mucho de la que aparecía en el tema anterior. La función general cuya gráfica era una línea recta podía tener la expresión 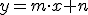 , donde m y n tenían cualquier valor, pues bien la función cuadrática solo se va a diferenciar en que tiene un sumando más con la variable al cuadrado.
, donde m y n tenían cualquier valor, pues bien la función cuadrática solo se va a diferenciar en que tiene un sumando más con la variable al cuadrado.
La expresión general de una función cuadrática es de la forma 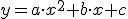 , donde a, b y c son números cualesquiera con la única condición de que a sea distinto de 0.
, donde a, b y c son números cualesquiera con la única condición de que a sea distinto de 0.
Todas las funciones de ese tipo tienen como gráfica una parábola.
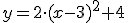 .
.
El problema se nos presenta cuando nos dan una función en la forma 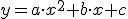 y queremos saber cuál es su eje y cuál su vértice para poderla representar. El proceso a seguir es el siguiente.
y queremos saber cuál es su eje y cuál su vértice para poderla representar. El proceso a seguir es el siguiente.
a) Cálculo del eje. El eje de la parábola nos la da la expresión 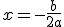 .
.
b) Cálculo del vértice. La abscisa del vértice ya la tenemos pues es el valor anterior, para hallar la otra componente basta sustituir en la función y hallar su valor.
c) Cálculo de otros puntos. Una vez fijado el vértice, sólo nos falta saber cómo se comporta la función en puntos cercanos a él. Lo usual es hallar los puntos de corte con los ejes ya que esos puntos nos dan mucha información. Ya en el tema 2 viste cómo hallar esos puntos.
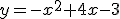 realizando el estudio previo de los valores importantes.
realizando el estudio previo de los valores importantes.
Las funciones cuadráticas tienen un dominio igual al conjunto de los reales 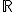 , es decir, cualquier valor se puede sustituir en la función.
, es decir, cualquier valor se puede sustituir en la función.
Si el coeficiente a es positivo, la función primero es decreciente, en el vértice tiene el mínimo absoluto y después es creciente. Su recorrido va por tanto desde el valor del vértice hasta 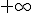 .
.
Si el coeficiente a es negativo, la función primero es creciente,
en el vértice tiene el máximo absoluto y después es decreciente. Su
recorrido va por tanto desde el valor 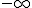 hasta el del vértice.
hasta el del vértice.
| |
|
| a > 0 |
a < 0 |
Representa varias funciones cuadráticas en la siguiente escena.
Tienes que mover los tres puntos que aparecen, con la única restricción de que el punto verde tiene que estar en el eje OY, o sea, el valor de la función cuando "x" vale cero.
Applet de Joaquín García Mollá en i-matematicas.com bajo licencia Creative Commons.
Para practicar te vamos a proponer dos actividades de la profesora Consolación Ruiz tomadas de su trabajo sobre Funciones polinómicas, a cuyo trabajo completo puedes acceder desde el enlace que hemos puesto en el título.
En la primera debes reconocer la gráfica de la función que aparece. Decide qué color corresponde y pulsa la letra correspondiente que aparece en la parte inferior. Realiza varios ejemplos hasta que domines bien el tema. Te damos como pista que te fijes en si los coeficientes de la x² son positivos o negativos, en el signo y valor que tiene el eje y en que punto corta al eje vertical, para ello basta que te fijes en el término independiente de la función.
El dueño de una papelería ha recibido una remesa de bolígrafos dedicados a la serie de televisión El Internado. Sabe que si los vende a 3 euros puede vender unos 20 ejemplares a la semana. Para ganar más dinero decide subir los precios pero observa que por cada 50 céntimos más que aumente el precio vende dos bolígrafos menos.
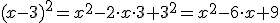
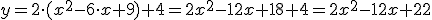
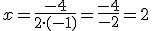
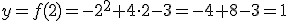 por lo que vale V(2,1).
por lo que vale V(2,1).
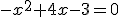 (suponemos que lo recuerdas de la Unidad 2) y obtenemos los puntos (1,0) y (3,0).
(suponemos que lo recuerdas de la Unidad 2) y obtenemos los puntos (1,0) y (3,0).