1.1. El lanzamiento se vuelve gráfica.
Ya te vas dando cuenta que en muchos aspectos de nuestro entorno podemos encontrar elementos que recorren líneas que no son paralelas, ¿eres consciente de ello? Muchos de estos recorridos curvos aparecen cuando en la función encontramos la variable elevada al cuadrado.
Cuando la variable x se eleva al cuadrado aparece un curva que recibe el nombre de parábola ¿a que la recuerdas de años anteriores? por eso el recorrido de objetos siguiendo esa línea suele llamarse tiro parabólico. Lo encontramos en los caños de las fuentes, siempre que se lance un proyectil de forma oblicua y en multitud de deportes: al meter un gol de volea, en voleibol al realizar algunos tiros, al lanzar un balón a la canasta de baloncesto. Incluso hay veces que no es un balón quien recorre la curva parabólica, sino el propio deportista como puedes apreciar en el siguiente vídeo.
Veamos ahora un ejemplo donde aparece esta función.
Nuestro amigo Esteban está juntando dinero para comprarse un iPod. De pronto aparece una oferta y quiere aprovecharla, pero al hacer recuento observa que le faltan 100 euros. Consigue que su padre se los preste con el compromiso de devolvérselos. Como al principio va a tener más problemas hasta que empiece a ahorrar, le propone a su padre darle 1 euro la primera semana, 3 la segunda, 5 la tercera y así sucesivamente hasta condonar la deuda.
Rellena la siguiente tabla colocando en cada celda lo que ha entregado hasta ese momento a su padre, para así saber cuando ha cubierto la deuda completa.
Atención: en la tabla no debes colocar lo que entrega cada semana sino lo que ha entregado en total a su padre hasta ese momento.
| nº de semana | 1 | 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| entregado hasta el momento |
|
|
|
|
|
|
|
|
|
| |
Si los valores que has obtenido en la tabla anterior los representamos en unos ejes de coordenadas, obtenemos la siguiente gráfica. La línea discontinua no tendría sentido dibujarla en este caso, sólo lo hacemos para que veas cuál es la evolución real de los valores de la función.
Como ves por la tabla o la gráfica a cada valor le corresponde precisamente su cuadrado, quiere decir que en este caso podemos encontrar fácilmente su expresión algebraica que sería 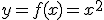 .
.
| |
La parábola es una gráfica con la característica de ser continua y simétrica respecto a una recta vertical que recibe el nombre de eje de la parábola. El punto donde la parábola corta a ese eje se llama vértice y suele ser el mayor o menor valor que toma la función.
En la gráfica siguiente tiene la gráfica de la función cuadrática más simple 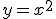 .
.
 |
|
1. Imagen de Facundo Fernández bajo licencia Creative Commons
|
Hay muchos aspectos creados por el hombre en el que aparece la parábola, por ejemplo en los faros de los coches o en nuestras cotidianas antenas parabólicas con las que podemos acceder a la televisión vía satélite.
 |