1.2. Tuneando la parábola clásica.
 |
Al trabajar el punto anterior te puede haber pasado un pensamiento por la cabeza: "esta gente se está quedando conmigo, tanto hablar de tiros parabólicos, de lanzar balones a canastas y chorros de agua, pero ahora la gráfica que se presenta por parábola no se parece a los recorridos del agua o de los balones". El motivo es porque la gráfica del apartado anterior es la más básica, la que aparece al darle valores a la función 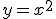 .
.
Ya en el tema anterior viste que una recta podía tener muchas presentaciones, unas veces era creciente, otras decreciente, a veces constante. En este caso va a pasar igual, la parábola tiene una forma característica pero puede presentarse de distintas formas.
Para trabajar en este apartado vamos a utilizar la siguiente actividad de Geogebra, y manipulando con ella queremos que tú seas quien descubra las variaciones de esta función. Como en otras actividades anteriores, tiene tres deslizadores que en cada momento te iremos explicando qué representan. De entrada tienes dibujada la parábola básica.
El deslizador "a" va a representar un coeficiente por el que multiplicamos la x². Es decir, mientras mantengamos h=s=0, vamos a representar la función  .
.
Verdadero Falso
Verdadero Falso
Verdadero Falso
Verdadero Falso
 . Como podrás apreciar, al mover el deslizador, esa h corresponde al valor del eje de la parábola. Recuerda que la gráfica es simétrica respecto de ese eje.
. Como podrás apreciar, al mover el deslizador, esa h corresponde al valor del eje de la parábola. Recuerda que la gráfica es simétrica respecto de ese eje.
Cuando le resto un número a la variable en la función cuadrática, el efecto es que el eje de la parábola se traslada horizontalmente y por tanto toda la gráfica.
¿Hacia adonde se traslada la gráfica?
Ya has comprobado que restarle un número a la variable tiene el efecto de que la gráfica se mueve horizontalmente, vamos a ver otro movimiento. Para ello vuelve a dejar h=0.
Ahora vamos a utilizar el valor de s. Esa cantidad se la vamos a sumar a la función, es decir, la gráfica está preparada para representar la función 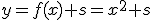 .
.
Mueve el deslizador s y contesta a la pregunta.
¿Hacia adonde se traslada la gráfica de la función?
Por último, mueve los deslizadores que quieras para obtener cualquier función. Observa que el vértice siempre tiene las coordenadas V(h,s). La expresión que se está representando tiene la forma general dada por 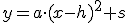 .
.
Puedes comprobarlo colocando el ratón sobre la función y pulsando el botón derecho. En el menú que te aparece elige la opción Propiedades y en la nueva ventana que aparece debes activar la opción Expone rótulo y dentro de la ventana desplegable siguiente elegir la opción Valor. De esa forma verás la ecuación de la gráfica en todo momento.
Para terminar este apartado practica lo aprendido realizando las siguientes actividades de Jclic.(3 actividades o pantallas distintas)
 |
En la vida cotidiana hay un tipo de curva que suele confundirse con la parábola y que también es muy corriente. Por ejemplo si te has fijado en la carretera en dos postes de luz o de teléfonos, la línea que forman los cables recibe el nombre de catenaria. En la siguiente lámina puedes aprender de donde surge y qué discusión histórica se creó entre los principales matemáticos de la época con respecto a otra curva famosa, la cicloide.